
如图,Rt△ABO在直角坐标系中,AB⊥x轴于点B,AO=10,sin∠AOB=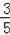
 ,反比例函数y=
,反比例函数y=
 (x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .
(x>0)的图象经过AO的中点C,且与AB交于点D,则BD= .


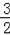
 .
.
【考点】反比例函数图象上点的坐标特征.
【专题】计算题.
【分析】先根据正弦的定义求出AB=6,再利用勾股定理计算出OB=8,则A点坐标为(8,6),由于C点为OA的中点,所以C点坐标为(4,3),根据反比例函数图象上点的坐标特征得到反比例函数解析式为y=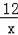
 ,再确定D点坐标,即可得到BD的长.
,再确定D点坐标,即可得到BD的长.
【解答】解:∵AB⊥x轴于点B,
∴∠ABO=90°
∴sin∠AOB=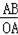
 =
=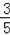
 ,而OA=10,
,而OA=10,
∴AB=6,
∴OB=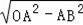
 =8,
=8,
∴A点坐标为(8,6),
∵C点为OA的中点,
∴C点坐标为(4,3),
∴k=3×4=12,
∴反比例函数解析式为y=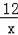
 ,
,
把x=8代入得y=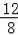
 =
=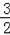
 ,
,
∴D点坐标为(8,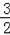
 ),
),
∴BD=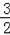

故答案为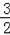
 .
.
【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数y=
 (k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.
(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
已知关于x的方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)当该方程的一个根为1时,求a的值及方程的另一根.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,则△PEB的周长的最小值是 .
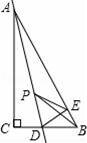

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
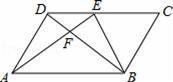

A.2:3 B.2:5 C.3:5 D.3:2
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
| x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
| y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为(﹣2,0);②抛物线与y轴的交点为(0,6);③抛物线的对称轴是x=1;④在对称轴左侧y随x增大而增大.
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
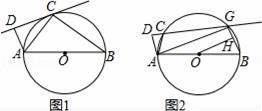
如图1,AB为⊙O的直径,C为⊙O上一点,作AD⊥CD,垂足为D.
(1)若直线CD与⊙O相切于点C,求证:△ADC∽△ACB;
(2)如果把直线CD向下平行移动,如图2,直线CD交⊙O于C、G两点,若题目中的其他条件不变,tan∠DAC=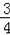
 ,AB=10,求圆心O到GB的距离OH的长.
,AB=10,求圆心O到GB的距离OH的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
华盛公司有甲、乙两个销售团队,同时销售同种产品,12个月后统计得出如下信息:甲销售团队第x个月销售量y1(万件)与x之间的函数关系为y1=a(x﹣4)2+
 ;乙销售团队第x个月销售量y2(万件)与x之间的函数关系为y2=kx+1(1≤x≤12,x为整数).甲、乙两个销售团队在第1个月的销售量相同,均为
;乙销售团队第x个月销售量y2(万件)与x之间的函数关系为y2=kx+1(1≤x≤12,x为整数).甲、乙两个销售团队在第1个月的销售量相同,均为
 (万件)
(万件)
(1)分别求y1、y2的函数解析式;
(2)探求有几个月乙销售团队比甲销售团队的销量高,并求当月最多高出多少万件?
(3)直接写出共有多少个月甲、乙两个销售团队的销售量均不低于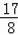
 万件.
万件.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com