练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
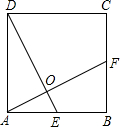
    如图，正方形ABCD中，AF⊥DE于点O，tan∠FAB=
    1
    2
    ，则
    AO
    DO
    等于
     
    ．
    考点：正方形的性质,锐角三角函数的定义
    专题：
    分析：根据同角的余角相等求出∠ADO=∠FAB，然后根据锐角三角函数的定义解答即可．
    解答：解：∵AF⊥DE，
    ∴∠ADO+∠DAO=90°，
    在正方形ABCD中，∠BAD=90°，
    ∴∠DAO+∠FAB=90°，
    ∴∠ADO=∠FAB，
    ∴tan∠FAB=tan∠ADO=
    AO
    DO
    =
    1
    2
    ．
    故答案为：
    1
    2
    ．
    点评：本题考查了正方形的性质，锐角三角函数的定义，熟记性质并利用同角的余角相等求出∠ADO=∠FAB是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    计算：
    （1）1-2+3-4+…+2009-2010+2011-2012+2013-2014；
    （2）（-8）+（0.25）-（-9）+（-
    1
    4
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    △ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边．
    （1）若a=5，b=12，则c=
     
    ； 
    （2）若∠A=30°，a=1，则b=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

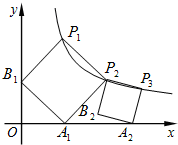    正方形的A1B1P1P2顶点P1、P2在反比例函数y=
    8
    x
    （x＞0）的图象上，顶点A1、B1分别在x轴、y轴的正半轴上，再在其右侧作正方形P2P3A2B2，顶点P3在反比例函数y=
    8
    x
    （x＞0）的图象上，顶点A2在x轴的正半轴上，求点P3的坐标
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，△ABC与△AEF中，AB=AE，BC=EF，∠B=∠E，AB交EF于D．给出下列结论：
    ①∠AFC=∠C；②DF=CF；③BC=DE+DF；④∠BFD=∠CAF．
    其中正确的结论是
     
    （填写所有正确结论的序号）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一个曲面和一个圆完成的几何体是
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在图中，每个图案均由边长为1的小正方形按一定的规律堆叠而成，照此规律，第100个图案中共有
     
    个小正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列各对数值是二元一次方程
    1
    2
    x-y=6的解的是（　　）
    A、
    x=-8
    y=10
    B、
    x=8
    y=2
    C、
    x=10
    y=-1
    D、
    x=2
    y=5

    查看答案和解析>>

    科目：初中数学 来源： 题型：

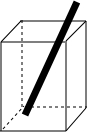    如图，将一根长为20cm的玻璃棒放入一个长为4cm，宽为3cm，高为12cm的长方形容器中，你知道玻璃棒露在外面的部分的长度d在什么范围之内吗？请通过计算写出d的范围．

    查看答案和解析>>

    同步练习册答案