
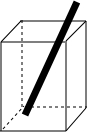
 如图,将一根长为20cm的玻璃棒放入一个长为4cm,宽为3cm,高为12cm的长方形容器中,你知道玻璃棒露在外面的部分的长度d在什么范围之内吗?请通过计算写出d的范围.
如图,将一根长为20cm的玻璃棒放入一个长为4cm,宽为3cm,高为12cm的长方形容器中,你知道玻璃棒露在外面的部分的长度d在什么范围之内吗?请通过计算写出d的范围. 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
 如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=
如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽”(a),中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高”(h).我们可得出一种计算三角形面积的新方法:S△ABC=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
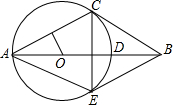 在△ABC中,tanA=
在△ABC中,tanA=| 1 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com