
【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:![]() ,
,![]() ,求:
,求:![]() 的值;
的值;
②已知:![]() ,
,![]() ,求:
,求:![]() 的值.
的值.
【答案】(1)方法1:(m﹣n)2;方法2:(m+n)2﹣4mn;
(2)(m﹣n)2;(m+n)2﹣4mn;(m﹣n)2=(m+n)2﹣4mn;
(3)①1;②3.
【解析】试题分析:(1)表示出阴影部分的边长,然后利用正方形的面积公式列式;
利用大正方形的面积减去四周四个矩形的面积列式;
(2)根据不同方法表示的阴影部分的面积相同解答;
(3)根据(2)的结论代入进行计算即可得解.
解:(1)方法1:(m﹣n)2;
方法2:(m+n)2﹣4mn;
(2)(m﹣n)2=(m+n)2﹣4mn;
故答案为:(m﹣n)2;(m+n)2﹣4mn;(m﹣n)2=(m+n)2﹣4mn;
(3)①解:∵a﹣b=5,ab=﹣6,
∴(a+b)2=(a﹣b)2+4ab=52+4×(﹣6)=25﹣24=1;
②解:由已知得:(a+)2=(a﹣)2+4a=12+8=9,
∵a>0,a+>0,
∴a+=3.


科目:初中数学 来源: 题型:
【题目】据国家新闻出版广电总局电影局数据,2017年国庆中秋节假期全国城市影院电影票房约26亿元,总票房创下该档期新纪录,26亿用科学记数法表示正确的是 ( )
A. 26×108 B. 2.6×108 C. 26×109 D. 2.6×109
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线![]() 相交于A(1,
相交于A(1,![]() ),B(4,0)两点.
),B(4,0)两点.
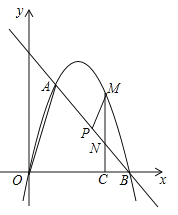
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN,求出![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
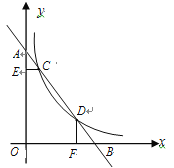
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,与双曲线
,与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)求直线![]() 的解析式;
的解析式;
(3)求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com