
【题目】如图,在Rt△ABC中,∠ACB=90![]() ,CD
,CD![]() AB于D.
AB于D.

(1)写出图中相似的三角形;
(2)求证: ![]() = AD·BD .
= AD·BD .
【答案】(1)△ABC∽△ACD;△ABC∽△CBD; △ACD∽△CBD(2)证明见解析.
【解析】试题分析:(1)利用两组角相等即可得到两个三角形相似,可找到所有相似的三角形;
(2)利用(1)中的△ADC∽△CDB,可得到结论.
试题解析:解:(1)∵∠ACB=90°,CD⊥AB,∴∠A+∠B=∠BCD+∠B,∴∠A=∠BCD,且∠ADC=∠CDB,∴△ADC∽△CDB,在△ADC和△ACB中,∠A=∠A,∠ADC=∠ACB,∴△ADC∽△ACB,同理可得△CDB∽△ACB,∴图中所有相似的三角形有:△ADC∽△CDB,△ADC∽△ACB,△CDB∽△ACB;
(2)∵△ADC∽△CDB,∴ ![]() ,∴CD2=ADDB.
,∴CD2=ADDB.


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
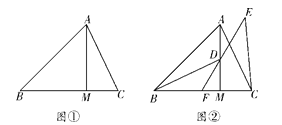
【题目】在△ABC中,∠ABM=45°,AM⊥BM,垂足为M,点C是BM延长线上一点,连接AC.
(1)如图①,若AB=3![]() ,BC=5,求AC的长;
,BC=5,求AC的长;
(2)如图②,点D是线段AM上一点,MD=MC,点E是△ABC外一点,EC=AC,连接ED并延长交BC于点F,且点F是线段BC的中点,求证:∠BDF=∠CEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,已知直线![]() 和双曲线
和双曲线![]() (k>0),点A(m,n)在双曲线
(k>0),点A(m,n)在双曲线 ![]() 上.当m=n=2时.
上.当m=n=2时.
(1)直接写出k的值;
(2)将直线![]() 作怎样的平移能使平移后的直线与双曲线
作怎样的平移能使平移后的直线与双曲线 ![]() 只有一个交点.
只有一个交点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)抛物线![]() 经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
经过点A (4,0),点B (1,-3) ,求该抛物线的解析式;
(2)如图,要修建一个圆形喷水池,在池中心竖直安装一根水管,在水管的顶端安一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离池中心3m,水管应多长?

(3)如图,点P![]() (
(![]() >0),在
>0),在![]() 轴正半轴上,过点P作平行于
轴正半轴上,过点P作平行于![]() 轴的直线,分别交抛物线
轴的直线,分别交抛物线![]() 于点A,B,交抛物线
于点A,B,交抛物线![]() 于点C,D,求
于点C,D,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() 与
与![]() 轴交于点A,点B(1,0),与
轴交于点A,点B(1,0),与![]() 轴交于点C(0,﹣3),点M是其顶点.
轴交于点C(0,﹣3),点M是其顶点.
(1)求抛物线解析式;
(2)第一象限抛物线上有一点D,满足∠DAB=45°,求点D的坐标;
(3)直线![]() (﹣3<
(﹣3<![]() <﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
<﹣1)与x轴相交于点H.与线段AC,AM和抛物线分别相交于点E,F,P.证明线段HE,EF,FP总能组成等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y1=-x-2交x轴于点A,交y轴于点B,抛物线y2=ax2+bx+c的顶点为A,且经过点B.
(1)求该抛物线的解析式;
(2)求当y1≥y2时x的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
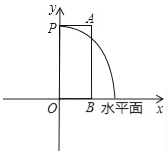
【题目】某市人民广场上要建一个圆形的喷水池,并在水池中央垂直安装一个柱子OP,柱子顶端P处装上喷头,由P处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示).若已知OP=3米,喷出的水流的最高点A距水平面的高度是4米,离柱子OP的距离为1米.
(1)求这条抛物线的解析式;
(2)若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中错误的是( )
A.某种彩票的中奖率为1%,买100张彩票一定有1张中奖
B.从装有10个红球的袋子中,摸出1个白球是不可能事件
C.为了解一批日光灯的使用寿命,可采用抽样调查的方式
D.掷一枚普通的正六面体骰子,出现向上一面点数是2的概率是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com