
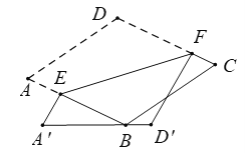
【题目】如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点![]() ,
,![]() 处,且
处,且![]() 经过点B,EF为折痕,当
经过点B,EF为折痕,当![]() ⊥CD时,
⊥CD时,![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
延长DC和![]() ,两延长线相交于点G,利用菱形的性质可证得∠A=∠DCB=60°,AB=BC=DC,利用折叠的性质可得到∠D=∠
,两延长线相交于点G,利用菱形的性质可证得∠A=∠DCB=60°,AB=BC=DC,利用折叠的性质可得到∠D=∠![]() F=120°,DF=
F=120°,DF=![]() F,再证明∠CBG=∠G=30°,利用等角对等边可得到BC=CG,设CF=x,DF=y,用含x,y的代数式表示出DC,CG,FG的长,然后在Rt△
F,再证明∠CBG=∠G=30°,利用等角对等边可得到BC=CG,设CF=x,DF=y,用含x,y的代数式表示出DC,CG,FG的长,然后在Rt△![]() FG中,利用解直角三角形可得到x与y的关系式,据此可求出CF与DF的比值.
FG中,利用解直角三角形可得到x与y的关系式,据此可求出CF与DF的比值.
解:延长DC和![]() ,两延长线相交于点G,
,两延长线相交于点G,
∵菱形ABCD,∠A=60°,
∴∠A=∠DCB=60°,AB=BC=DC
∴∠BCG=180°-60°=120°,
∵将纸片折叠,点A,D分别落在点![]() 处,且
处,且![]() 经过点B,EF为折痕,
经过点B,EF为折痕,
∴∠D=∠![]() F=120°,DF=
F=120°,DF=![]() F
F
∵![]() F⊥DC,
F⊥DC,
∴∠![]() FG=90°,
FG=90°,
∴∠G=90°-60°=30°
∴∠CBG=180°-∠G-∠BCG=180°-30°-120°=30°
∴∠CBG=∠G
∴BC=CG,
设CF=x,DF=y,则DC=CG=x+y
∴FG=2x+y,
在Rt△![]() FG中,
FG中,
![]()
![]()
![]()
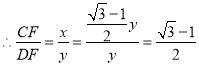 .
.
故选:A.


科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线![]() 交AB,BC分别于点M,N,反比例函数
交AB,BC分别于点M,N,反比例函数![]() 的图象经过点M,N.
的图象经过点M,N.

(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ABC=90°
(1)如图1,分别过A、C两点作经过点B的直线的垂线,垂足分别为点M,N,求证:△ABM∽△BCN;
(2)如图2,P是BC边上一点,∠BAP=∠C,tan∠PAC=![]() ,BP=2cm,求CP的长.
,BP=2cm,求CP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“村村通公路政策,是近年来国家构建和谐社会,支持新农村建设的一项重大公共决策,是一项民心工程,惠民工程某镇政府准备向甲、乙两个工程队发包一段“村村通”工程建设项目,经调查:甲、乙两队单独完成该工程,乙队所需时间是甲队的2倍;甲、乙两队共同完成该工程需30天;若甲队每天所需劳务费用为2400元,乙队每天所需劳务费用为1500元,从节约资金的角度考虑,应选择哪个工程队更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】投石机是古代的大型攻城武器,是数学、工程、物理等复杂学科相互融合的应用(如图(1)).在我国《元史·亦思马因传》中对这种投石机就有过记载(如图(2)).
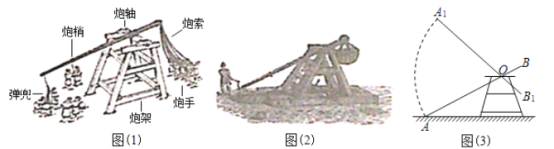
图(3)是图(1)中人工投石机的侧面示意图,炮架的横向支架均与地面相互平行,已知![]() 米,炮轴距地面4.5米,
米,炮轴距地面4.5米,![]()
![]() ,炮梢顶端点
,炮梢顶端点![]() 能到达水平地面,最高点能到达点
能到达水平地面,最高点能到达点![]() 处,且旋转的夹角
处,且旋转的夹角![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 在同一平面内),求点
在同一平面内),求点![]() 到水平地面的距离.(参考数据:
到水平地面的距离.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为半圆O的直径,AC是⊙O的一条弦,D为![]() 的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
的中点,作DE⊥AC于点E,交AB的延长线于点F,连结AD.
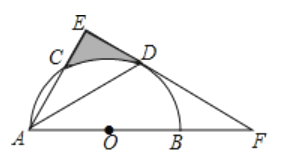
(1)求证:EF为半圆O的切线.
(2)若AO=BF=2,求阴影区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=x+m的图象与反比例函数y=![]() 的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
的图象交于A,B两点,且与x轴交于点C,点A的坐标为(2,1).
(1)求m及k的值;
(2)求点C的坐标,并结合图象写出不等式组0<x+m≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com