
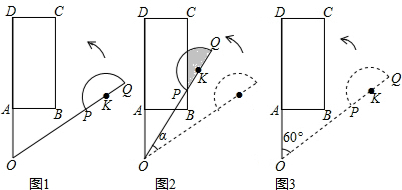
分析 (1)如图1所示,过点P作PA′⊥OD,垂足为A′.在△A′OP中利用利用特殊锐角三角函数可求得OA′=1,由OA=1,从而可求得点A与点A′重合,根据过一点有且只有一条直线与已知直线垂直可知点P在AB上;如图2所示:由△ABO为等腰直角三角形可知∠AOB=45°,从而可求得∠QOQ′=15°;
(2)如图3所示:过点P作PE⊥OD,垂足为E,过点K作KG⊥PF,连接KF.依据特殊锐角三角函数可知:∠POE=30°.由平行线的性质可知∠AOP=∠OPB=30°,于是得到∠FPQ=30°,由圆周角定理可知∠FKQ=60°,然后依据扇形的面积公式可求得扇形KKQ的面积=$\frac{1}{6}π×(\frac{1}{2})^{2}$=$\frac{π}{24}$,然后利用特殊锐角三角函数求得GK和FG的长,从而可求得△FPK的面积=$\frac{\sqrt{3}}{16}$;
(3)如图4所示:连接AQ,过点Q作QE⊥AB,垂足为E.由∠AOQ=60°,可知∠EQO=60°.由特殊锐角三角函数可知QE=$\frac{1}{2}$PQ=$\frac{1}{2}×1$=$\frac{1}{2}$,AE=$\frac{3\sqrt{3}}{2}$,在Rt△AQE中由勾股定理得AQ=$\sqrt{7}$.如图5所示:F为半圆与CB的切线,延长KF交OD于G,连接AK交半圆与点E.由切线的性质可知:KG⊥OD,故此可知:GK=1.5,在Rt△OGK中,由勾股定理可知OG=2,于是得到AG=1,在Rt△AKG中,由勾股定理可知AK=$\frac{\sqrt{13}}{2}$,AE=AK-EK=$\frac{\sqrt{13}-1}{2}$.从而可得到$\frac{\sqrt{13}-1}{2}≤d≤\sqrt{7}$.
解答 解:(1)如图1所示,过点P作PA′⊥OD,垂足为A′.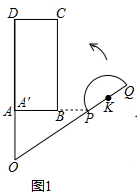
∵PA′⊥OD,
∴∠PA′O=90°.
∵∠POA′=60°,
∴OA′=cos60°•OP=$\frac{1}{2}OP$=$\frac{1}{2}×$2=1.
又∵OA=1,
∴点A与点A′重合.
∵PA⊥OD,AB⊥OD,
∴点P在直线AB上.
如图2所示: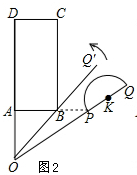
∵AB=OA,∠OAB=90°,
∴∠AOB=45°.
∵∠AOP=60°,
∴∠QOQ′=60°-45°=15°.
故答案为:在;15°.
(2)如图3所示:过点P作PE⊥OD,垂足为E,过点K作KG⊥PF,连接KF.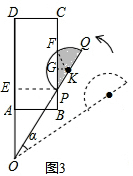
∵PE⊥OD,
∴∠PEO=90°.
∵$\frac{EP}{OP}=\frac{1}{2}$,
∴∠POE=30°.
∵OD∥BC,
∴∠AOP=∠OPB=30°.
∴∠FPQ=30°.
∴∠FKQ=60°.
∴扇形KKQ的面积=$\frac{1}{6}π×(\frac{1}{2})^{2}$=$\frac{π}{24}$.
∵KP=$\frac{1}{2}$,∠GPK=30°,
∴KG=$\frac{1}{4}$,GP=$\frac{\sqrt{3}}{4}$.
∴FP=$\frac{\sqrt{3}}{2}$
∴△FPK的面积=$\frac{1}{2}×\frac{\sqrt{3}}{2}×\frac{1}{4}$=$\frac{\sqrt{3}}{16}$.
∴阴影部分的面积=$\frac{\sqrt{3}}{16}+\frac{π}{24}$.
(3)如图4所示:连接AQ,过点Q作QE⊥AB,垂足为E.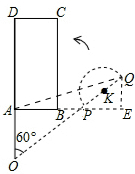
∵AB⊥OD,
∴∠BAO=90°.
又∵∠AOQ=60°,
∴∠APO=30°.
∴∠QPE=30°.
∴QE=$\frac{1}{2}$PQ=$\frac{1}{2}×1$=$\frac{1}{2}$,PE=$\frac{\sqrt{3}}{2}PQ$=$\frac{\sqrt{3}}{2}$,AP=$\frac{\sqrt{3}}{2}OP$=$\sqrt{3}$.
∴AE=$\frac{\sqrt{3}}{2}QE+\frac{\sqrt{3}}{2}AO$=$\frac{\sqrt{3}}{2}×(1+\frac{1}{2})$=$\frac{3\sqrt{3}}{2}$.
∴AQ=$\sqrt{A{E}^{2}+Q{E}^{2}}$=$\sqrt{(\frac{3\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}}$=$\sqrt{7}$.
如图5所示:F为半圆与CB的切线,延长KF交OD于G,连接AK交半圆与点E.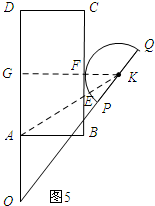
∵半圆与BC相切,切点为F,
∴KF⊥BC.
∴KG⊥OD.
∴GK=GF+FK=1+0.5=1.5.
在Rt△OGK中,OG=$\sqrt{O{K}^{2}-G{K}^{2}}$=2.
∵OA=1,
∴AG=1.
在Rt△AKG中,AK=$\sqrt{G{K}^{2}+A{G}^{2}}$=$\frac{\sqrt{13}}{2}$.
∴AE=AK-EK=$\frac{\sqrt{13}}{2}$-$\frac{1}{2}$=$\frac{\sqrt{13}-1}{2}$.
∴$\frac{\sqrt{13}-1}{2}≤d≤\sqrt{7}$.
点评 本题主要考查的是圆的综合应用、特殊锐角三角函数的应用、勾股定理、切线的性质、等腰直角三角形的性质、圆周角定理、扇形的面积公式,根据题意画出d取值最大值和最小值时刻的图形是解题的关键.


科目:初中数学 来源: 题型:选择题
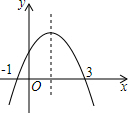 如图为二次函数y=ax2+bx+c(a≠0)的图象,对称轴是x=1,则下列说法:①b>0;②2a+b=0;③4a-2b+c>0;④3a+c>0;⑤m(ma+b)<a+b(常数m≠1).其中正确的个数为( )
如图为二次函数y=ax2+bx+c(a≠0)的图象,对称轴是x=1,则下列说法:①b>0;②2a+b=0;③4a-2b+c>0;④3a+c>0;⑤m(ma+b)<a+b(常数m≠1).其中正确的个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一个正方体的表面展开图,把展开图折叠成正方体后,与标号为1的顶点重合的是( )
如图是一个正方体的表面展开图,把展开图折叠成正方体后,与标号为1的顶点重合的是( )| A. | 标号为2的顶点 | B. | 标号为3的顶点 | C. | 标号为4的顶点 | D. | 标号为5的顶点 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com