
分析 利用[a]以及{a}=a-[a]的意义得出当x=2时,y=n,当x=2.5时,y=0.5m+n,进而利用函数y=m{x}+n的最小值为8,最大值为10,分别求出即可.
解答 解:∵{a}=a-[a],
∴{x}=x-[x],
∵$2≤x≤\frac{5}{2}$,
∴{x}=x-[x]=x-2
∴函数y=m{x}+n
=m(x-2)+n,
当x=2时,y=n,
当x=2.5时,y=0.5m+n,
∵函数y=m{x}+n的最小值为8,最大值为10,
∴当n=8时,0.5m+n=10,
解得:m=4,
则m+n=12,
当n=10时,0.5m+n=8,
解得:m=-4,
则m+n=6,
综上所述:m+n=6或12.
故答案为:6或12.
点评 此题主要考查了取整计算,根据定义得出y=m(x-2)+n进而分析得出是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 “无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.现将边长为a的正方形挖去一个边长为b的小正方形(a>b)(如图甲),把剩下的部分拼成一个矩形(如图乙).根据这两个图形中阴影部分的面积,能够验证的等式是( )| A. | a2-b2=(a+b)(a-b) | B. | (a-b)2=a2-2ab+b2 | ||
| C. | (a+2b)(a-b)=a2+ab-2b2 | D. | (a+b)2=a2+2ab+b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
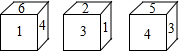 有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )
有一正方体,六个面上分别写有数字1、2、3、4、5、6,有三个人从不同的角度观察的结果如图所示.如果记1的对面的数字为a,3的对面的数字为b,那么a+b的值为( )| A. | 3 | B. | 7 | C. | 8 | D. | 11 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
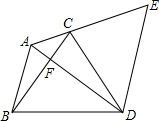 如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.
如图在△ABC中,∠BAC=120°,以BC边向形外作等边△BCD,把△ABC绕着点D顺时针方向旋转60°后得到△ECD,此时恰好A、C、E三点共线,连接AD和BC相交于点F.若AB=5,ED=8,则CF的长是$\frac{21}{8}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
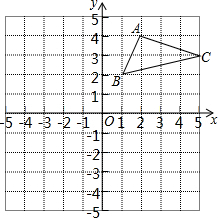 如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
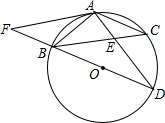 如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.
如图,在⊙O中,弦AB=AC,BD为⊙O的直径,AD交BC于E,AF∥BC交DB的延长线于点F,AE=2,ED=4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com