练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，二次函数y＝ax2＋bx＋c(a≠0)的图象与x轴交于A，B两点，与y轴交于点C，且OA＝OC.则下列结论：①abc＜0；②＞0；③ac－b＋1＝0；④OA·OB＝－.其中结论正确的是____________

    【答案】①③④

    【解析】（1）∵抛物线开口向下，

    ∴，

    又∵对称轴在轴的右侧，

    ∴，

    ∵抛物线与轴交于正半轴，

    ∴ ，

    ∴，即①正确；

    （2）∵抛物线与轴有两个交点，

    ∴，

    又∵，

    ∴，即②错误；

    （3）∵点C的坐标为，且OA=OC，

    ∴点A的坐标为，

    把点A的坐标代入解析式得： ，

    ∵，

    ∴，即③正确；

    （4）设点A、B的坐标分别为，则OA=，OB=，

    ∵抛物线与轴交于A、B两点，

    ∴是方程的两根，

    ∴，

    ∴OA·OB=.即④正确；

    综上所述，正确的结论是：①③④.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

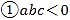
    科目：初中数学 来源： 题型：

    【题目】阅读下面内容，并按要求解决问题： 问题：“在平面内，已知分别有个点，个点，个点，5 个点，…，n 个点，其中任意三 个点都不在同一条直线上.经过每两点画一条直线，它们可以分别画多少条直线？ ” 探究：为了解决这个问题，希望小组的同学们设计了如下表格进行探究：（为了方便研 究问题，图中每条线段表示过线段两端点的一条直线）

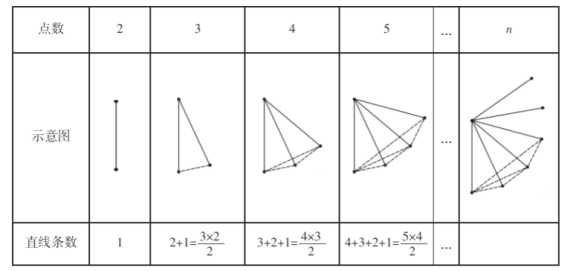
    请解答下列问题：

    （1）请帮助希望小组归纳，并直接写出结论：当平面内有个点时，直线条数为 ；

    （2）若某同学按照本题中的方法，共画了条直线，求该平面内有多少个已知点.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

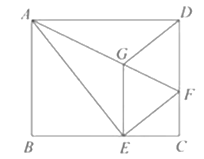
    【题目】如图，将矩形ABCD沿AF折叠，使点D落在BC边的点E处，过点E作EG∥CD交舡于点G，连接DG．

    (1)求证：四边形EFDG是菱形；

    (2) 求证： ；

    (3)若AG=6，EG=2，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

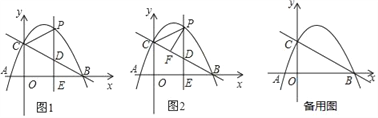
    【题目】如图1，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（﹣1，0）、B（4，0）两点，与y轴交于点C，且OC=3OA．点P是抛物线上的一个动点，过点P作PE⊥x轴于点E，交直线BC于点D，连接PC．

    （1）求抛物线的解析式；

    （2）如图2，当动点P只在第一象限的抛物线上运动时，求过点P作PF⊥BC于点F，试问△PDF的周长是否有最大值？如果有，请求出其最大值，如果没有，请说明理由．

    （3）当点P在抛物线上运动时，将△CPD沿直线CP翻折，点D的对应点为点Q，试问，四边形CDPQ是否成为菱形？如果能，请求出此时点P的坐标，如果不能，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】山西特产专卖店销售核桃，其进价为每千克40元，按每千克60元出售，平均每天可售出100千克，后来经过市场调查发现，单价每降低2元，则平均每天的销售可增加20千克，若该专卖店销售这种核桃要想平均每天获利2240元，请回答：

    （1）每千克核桃应降价多少元？

    （2）在平均每天获利不变的情况下，为尽可能让利于顾客，赢得市场，该店应按原售价的几折出售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：如图，抛物线与轴交于两点，点在抛物线上（点与两点不重合），如果的三边满足，则称点为抛物线的勾股点。

    ()直接写出抛物线的勾股点的坐标；

    ()如图，已知抛物线：与轴交于两点，点是抛物线的勾股点，求抛物线的函数表达式；

    ()在()的条件下，点在抛物线上，求满足条件的点（异于点）的坐标.

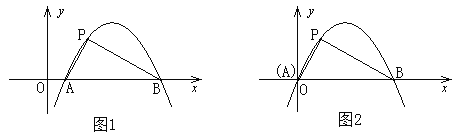
    查看答案和解析>>

    科目：初中数学 来源： 题型：

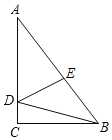
    【题目】在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D、E分别在AC、AB上，且△ADE是直角三角形，△BDE是等腰三角形，则BE=_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

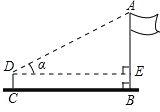
    【题目】某校九年级四个数学活动小组参加测量操场旗杆高度的综合实践活动，如图是四个小组在不同位置测量后绘制的示意图，用测角仪测得旗杆顶端A的仰角记为α，CD为测角仪的高，测角仪CD的底部C处与旗杆的底部B处之间的距离记为CB，四个小组测量和计算数据如下表所示：

    数据组别

    CD的长(m)

    BC的长(m)

    仰角α

    AB的长(m)

    第一组

    1.59

    13.2

    32°

    9.8

    第二组

    1.58

    13.4

    31°

    9.6

    第三组

    1.57

    14.1

    30°

    9.7

    第四组

    1.56

    15.2

    28°

    (1)利用第四组学生测量的数据，求旗杆AB的高度(精确到0.1m)；

    (2)四组学生测量旗杆高度的平均值约为　 　m(精确到0.1m)．

    (参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平行四边形ABCD中，点M在BC边上，且BM＝BC，AM与BD相交于点N，那么S△BMN：S平行四边形ABCD为（　　）

    A.1：3B.1：9C.1：12D.1：24

    查看答案和解析>>

    同步练习册答案