
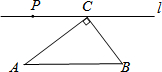
 如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC=6.4或10.
如图,在Rt△ABC中,AC=8,BC=6,直线l经过C,且l∥AB,P为l上一个动点,若△ABC与△PAC相似,则PC=6.4或10. 分析 先利用勾股定理求出AB的长,若△ABC与△PAC相似,则PC可以和AB对应也可以AC对应,所以要分两种情况分别讨论,求出PC的值即可.
解答 解:∵在Rt△ABC中,AC=8,BC=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10,
当△ABC≌△PCA时,则
AB:PC=AC:AC,
即10:PC=8:8,
解得:PC=10,
当△ABC∽ACP△时,则
AB:AC=AC:PC,
即10:8=8:PC,
解得:PC=6.4.
综上可知若△ABC与△PAC相似,则PC=6.4或10.
故答案为:6.4或10.
点评 本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.本题中把若干线段的长度用同一线段来表示是求线段是否成比例时常用的方法.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
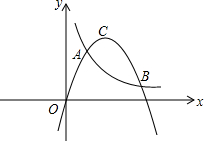 函数图象有一个公共点,我们就称两个函数图象“共一点”,有两个公共点,则称它们“共两点”…
函数图象有一个公共点,我们就称两个函数图象“共一点”,有两个公共点,则称它们“共两点”…查看答案和解析>>
科目:初中数学 来源: 题型:解答题
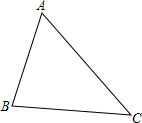 已知△ABC.
已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
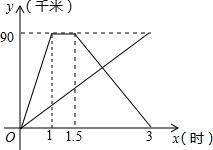 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com