
 ����ͼ����һ�������㣬���Ǿͳ���������ͼ��һ�㡱�������������㣬������ǡ������㡱��
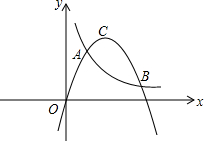
����ͼ����һ�������㣬���Ǿͳ���������ͼ��һ�㡱�������������㣬������ǡ������㡱������ ��1��������y=-x+bͼ���y=-x2+2xͼ��һ�㡱P�����Ӧ����-x+b=-x2+2x�����б�ʽΪ0�������b��ֵ�������������P�����ꣻ
��2��������y=-x+1ͼ���y=ax2+2xͼ�����㡱�����Ӧ����-x+1=ax2+2x�����б�ʽ��Ҫ����0�����������a��ȡֵ��Χ��
��3����A�ĺ�����Ϊm����ΪA��B����֮��ˮƽ����Ϊ2����B�ĺ�����Ϊm+2����������֮�䴹ֱ������A��y�����ĵ�������ɵù���m�ķ��̣��ⷽ�̿����m��ֵ�������ɵõ�A��B�����꣬�ٰ�A��B���������κ�������ʽ�����a��b��ֵ���̶��õ������߶���C�����꣮
��� �⣺��1���ߺ���y=-x+bͼ���y=-x2+2xͼ��һ�㡱��
��-x+b=-x2+2x����b2-4ac=9-4b=0��
��b=$\frac{9}{4}$��
��b=$\frac{9}{4}$ʱ��y=-x+$\frac{9}{4}$��-x+$\frac{9}{4}$=-x2+2x��
���x=$\frac{3}{2}$����x=$\frac{3}{2}$����y=-x+$\frac{9}{4}$����y=$\frac{3}{4}$��
��P������$\frac{3}{2}$��$\frac{3}{4}$����
��2���ߺ���y=-x+1ͼ���y=ax2+2xͼ�����㡱��
���Ӧ����-x+1=ax2+2x�����б�ʽ��Ҫ����0��
��9-4��a����-1����0
��ã�a��-$\frac{9}{4}$����a��0��
�ʴ�Ϊ��a��-$\frac{9}{4}$����a��0��
��3����A�ĺ�����Ϊm����B�ĺ�����Ϊm+2��
��A��B��y=$\frac{2}{x}$ ͼ���ϣ�
��A��B�ֱ��ʾΪ��m��$\frac{2}{m}$������m+2��$\frac{2}{m+2}$����
������֮�䴹ֱ������A��y�����ĵ�����
��$\frac{2}{m}$-$\frac{2}{m+2}$=$\frac{1}{m}$��
���m=2�������飬m=2��ԭ���̵ĸ���
��m=2ʱ��A��B�ֱ�Ϊ��2��1������4��$\frac{1}{2}$����
��A��B�ں���y=ax2+bxͼ���ϣ�
��1=4a+2b��$\frac{1}{2}$=16a+4b�����a=-$\frac{3}{16}$��b=$\frac{7}{8}$��
��y=-$\frac{3}{16}$x2+$\frac{7}{8}$x���䶥������CΪ��$\frac{7}{3}$��$\frac{49}{48}$����
���� ���⿼���˶��κ������ۺ�����Ŀ���õ���֪ʶ���к����������⡢һԪ���η��̸����б�ʽ���ⷽ���顢���ʽ���̣����������������ʣ���Ŀ���ۺ��Խ�ǿ����ѧ���ļ�������Ҫ��ܸߣ���Ŀ����ƱȽ���ӱ����һ���������п�ѹ���⣮


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д� ȫ�ų��100��ϵ�д�
ȫ�ų��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2+2ax+4x2 | B�� | -a2-4ax+4x2 | C�� | -2x+1+4x2 | D�� | x4+4+4x2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}+\sqrt{3}=\sqrt{5}$ | B�� | $\sqrt{2}•\sqrt{3}=\sqrt{6}$ | C�� | a6��a2=a3 | D�� | $\sqrt{��-2}{��^2}=-2$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
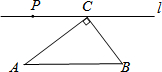 ��ͼ����Rt��ABC�У�AC=8��BC=6��ֱ��l����C����l��AB��PΪl��һ�����㣬����ABC���PAC���ƣ���PC=6.4��10��
��ͼ����Rt��ABC�У�AC=8��BC=6��ֱ��l����C����l��AB��PΪl��һ�����㣬����ABC���PAC���ƣ���PC=6.4��10���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 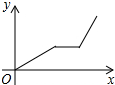 | B�� | 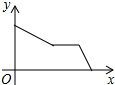 | C�� | 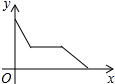 | D�� | 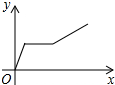 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
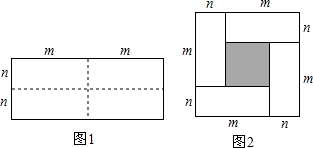
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ������һ�������尮����ʹ�õ�U�ͳأ���U�ͳؿ��Կ�����һ��������ȥ��һ������Բ�������ɣ��м�ɹ����в��ֵĽ����ǰ뾶Ϊ4m�İ�Բ�����ԵAB=CD=18m����E��CD�ϣ�CE=2cm��һ���а����ߴ�A�㵽E�㣬�ٴ�E�㻬�е�B�㣬�������е���̾����Ƕ��٣�����Ե���ֵĺ�ȿ��Ժ��Բ��ƣ���ȡ3��
��ͼ������һ�������尮����ʹ�õ�U�ͳأ���U�ͳؿ��Կ�����һ��������ȥ��һ������Բ�������ɣ��м�ɹ����в��ֵĽ����ǰ뾶Ϊ4m�İ�Բ�����ԵAB=CD=18m����E��CD�ϣ�CE=2cm��һ���а����ߴ�A�㵽E�㣬�ٴ�E�㻬�е�B�㣬�������е���̾����Ƕ��٣�����Ե���ֵĺ�ȿ��Ժ��Բ��ƣ���ȡ3���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com