
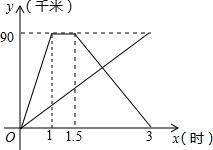
 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.分析 (1)首先设y与x之间的函数关系式为y=kx+b,根据图象可得直线经过(1.5,90),(3,0),利用待定系数法把此两点坐标代入y=kx+b,即可求出一次函数关系式;
(2)利用甲从B地返回A地的过程中,y与x之间的函数关系式算出y的值,即可得到108分钟时骑电动车所行驶的路程,再根据路程与时间算出电动车的速度,再用总路程90千米÷电动车的速度可得乙从A地到B地用了多长时间.
解答 解:(1)设甲从B地返回A地的过程中,y与x之间的函数关系式为y=kx+b,
根据题意得:$\left\{\begin{array}{l}{3k+b=0}\\{1.5k+b=90}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-60}\\{b=180}\end{array}\right.$,
所以y=-60x+180(1.5≤x≤3);
(2)∵当x=$\frac{108}{60}$=1.8时,y=-60×1.8+180=72,
∴骑电动车的速度为72÷1.8=40(千米/时),
∴乙从A地到B地用时为90÷40=2.25(小时)=135分钟.
点评 此题主要考查了一次函数的应用,关键是看懂图象所表示的意义,利用待定系数法求出甲从B地返回A地的过程中,y与x之间的函数关系式.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,
如图,在△ABC中,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
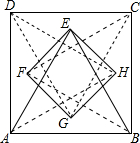 如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.
如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)
如图,这是一个供滑板爱好者使用的U型池,该U型池可以看作是一个长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是半径为4m的半圆,其边缘AB=CD=18m,点E在CD上,CE=2cm,一滑行爱好者从A点到E点,再从E点滑行到B点,则他滑行的最短距离是多少?(边缘部分的厚度可以忽略不计,π取3)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
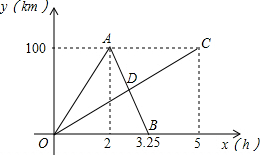 甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:
甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A种产品 | B种产品 | |
| 成本(万元/件) | 2 | 5 |
| 利润(万元/件) | 1 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com