
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
分析 (1)根据毛利润=(售价-进价)×销售量列出y与x的函数关系式即可;
(2)由甲种口罩的数量不多于乙种口罩数量的3倍,列出不等式解出自变量的取值范围即可确定函数值的最值.
解答 解:(1)根据题意得:y=(400-x)(22-18)+(9-6)x,
整理得:y=-x+1600;
(2)∵甲种口罩的数量不多于乙种口罩数量的3倍,
∴$\frac{400-x}{x}$≤3,
解得:x≥100,
由(1)得y=-x+1600,
∵k=-1<0,
∴函数值y随x的增大而减少,
∴使全部销售获得的毛利润最大,则x应取最小值,
∴当x=100时,y有最大值=1500.
点评 本题考查了一次函数的性质,列函数解析式,掌握一次函数的性质是解题的关键.


 步步高达标卷系列答案
步步高达标卷系列答案科目:初中数学 来源: 题型:解答题
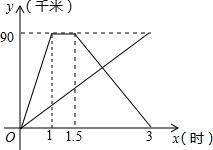 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
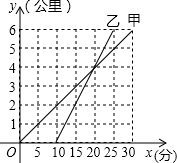 甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图.请你根据图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
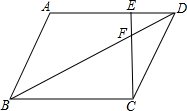 如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
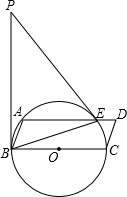 如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.
如图,BC为⊙O的直径,点A为⊙O上的点,以BC、AB为边作?ABCD,⊙O交于AD与点E,连接BE,点P是过点B的⊙O的切线上的一点.连结PE,且满足∠PEA=∠ABE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
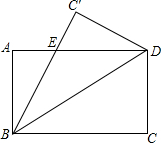 如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )
如图,把矩形纸片沿对角线BD折叠,设重叠部分为△EBD,则下列结论中错误的是( )| A. | ∠ABE=∠C′DE | B. | EB=ED | C. | EA=EC′ | D. | ∠ABE等于30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com