
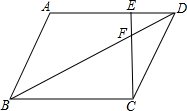
 如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
分析 根据题意得出△DEF∽△BCF,那么$\frac{EF}{CF}$=$\frac{ED}{CB}$;由AE:ED=2:1可设ED=k,得到AE=2k,BC=3k;得到$\frac{EF}{CF}$=$\frac{k}{3k}$,即可解决问题.
解答  解:如图,∵四边形ABCD为平行四边形,
解:如图,∵四边形ABCD为平行四边形,
∴ED∥BC,BC=AD;
∴△DEF∽△BCF,
∴$\frac{EF}{CF}$=$\frac{ED}{CB}$;
设ED=k,则AE=2k,BC=3k;
∴$\frac{EF}{CF}$=$\frac{k}{3k}$=$\frac{1}{3}$,
故选C.
点评 该题主要考查了相似三角形的判定与性质,平行四边形的性质等几何知识点及其应用问题;得出△DEF∽△BCF是解题的关键.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
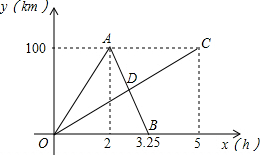 甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:
甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲 | 乙 | |
| 进价(元/个) | 18 | 6 |
| 售价(元/个) | 22 | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
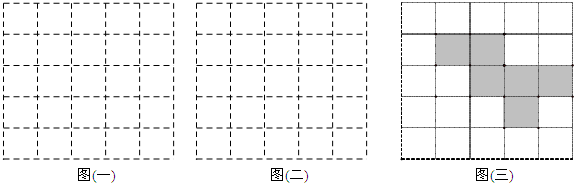
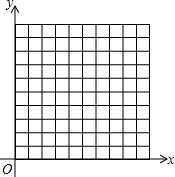 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.| P从O出发的时间 | 可以得到的整点的坐标 | 可以得到的整点的个数 |
| 1秒 | (0,1)、(1,0) | 2个 |
| 2秒 | (2,0)、(0,2)、(1,1) | 3 |
| 3秒 | (3,0)、(0,3)、(1,2)、(2,1) | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
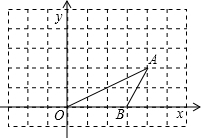 如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.
如图,点O、B的坐标分别为(0,0)、(3,0),将△OAB绕点O按逆时针方向旋转90°△OA′B′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com