
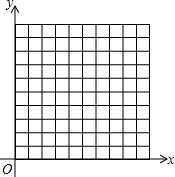
 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.| P从O出发的时间 | 可以得到的整点的坐标 | 可以得到的整点的个数 |
| 1秒 | (0,1)、(1,0) | 2个 |
| 2秒 | (2,0)、(0,2)、(1,1) | 3 |
| 3秒 | (3,0)、(0,3)、(1,2)、(2,1) | 4 |
分析 (1)根据运动的速度和只能向上或向右运动得到点的坐标;
(2)由规律得,出发1秒,得2个整点;出发2秒,得3个整点;出发3秒,得4个整点;…出发15秒时可得到16个整点;
(3)由规律得,出发1秒,得整点的坐标横纵坐标和为1;出发2秒,得整点的坐标横纵坐标和为2;出发3秒,得整点的坐标横纵坐标和为3,…横纵坐标和为17,得出发17秒.
解答 解:(1)根据运动的速度和只能向上或向右运动得到点的坐标为:(2,0)、(0,2)、(1,1),整点个数为3;
(2)出发1秒,得2个整点,
出发2秒,得3个整点,
出发3秒,得4个整点,
由规律得:
…出发15秒时可得到16个整点;
(3)出发1秒,得整点的坐标横纵坐标和为1,
出发2秒,得整点的坐标横纵坐标和为2,
出发3秒,得整点的坐标横纵坐标和为3,
由规律得:
…横纵坐标和为17,得出发17秒.
故答案为:(1)(2,0)、(0,2)、(1,1),3;
(2)16;
(3)17.
点评 本题主要考查了点的坐标的规律变化,利用点的坐标特点归纳规律是解答此题的关键.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:解答题
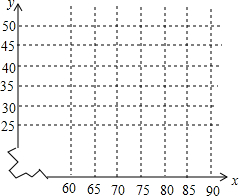 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
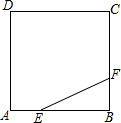 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
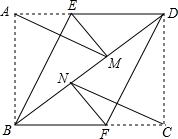 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
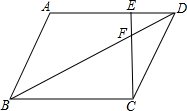 如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )
如图,在?ABCD中,点E在AD上,EC交对角线BD于点F,AE:ED=2:1,则EF:FC等于( )| A. | 1:1 | B. | 1:2 | C. | 1:3 | D. | 2:3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
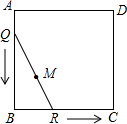 如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )
如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )| A. | $\frac{π}{4}$ | B. | 4-π | C. | π | D. | $\frac{4-π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com