
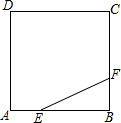
 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
分析 根据已知中的点E,F的位置,可知入射角的正切值为$\frac{1}{2}$,通过相似三角形,来确定反射后的点的位置,从而可得反射的次数.再由勾股定理就可以求出小球经过的路径的总长度.
解答 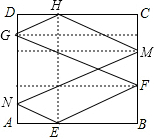 解:根据已知中的点E,F的位置,可知入射角的正切值为$\frac{1}{2}$,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得,$\frac{3}{2}$
解:根据已知中的点E,F的位置,可知入射角的正切值为$\frac{1}{2}$,第一次碰撞点为F,在反射的过程中,根据入射角等于反射角及平行关系的三角形的相似可得,$\frac{3}{2}$
第二次碰撞点为G,在DA上,且DG=$\frac{1}{6}$DA,
第三次碰撞点为H,在DC上,且DH=$\frac{1}{3}$DC,
第四次碰撞点为M,在CB上,且CM=$\frac{1}{3}$BC,
第五次碰撞点为N,在DA上,且AN=$\frac{1}{6}$AD,
第六次回到E点,AE=$\frac{1}{3}$AB.
由勾股定理可以得出EF=$\sqrt{5}$,FG=$\frac{3}{2}$$\sqrt{5}$,GH=$\frac{1}{2}$$\sqrt{5}$,HM=$\sqrt{5}$,MN=$\frac{3}{2}$$\sqrt{5}$,NE=$\frac{1}{2}$$\sqrt{5}$,
∴小球经过的路程为:$\sqrt{5}$+$\frac{3}{2}$$\sqrt{5}$+$\frac{1}{2}$$\sqrt{5}$+$\sqrt{5}$+$\frac{3}{2}$$\sqrt{5}$+$\frac{1}{2}$$\sqrt{5}$=6$\sqrt{5}$,
∴当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为6$\sqrt{5}$(n-1)+$\sqrt{5}$=6$\sqrt{5}$n-5$\sqrt{5}$,
故选C.
点评 本题主要考查了反射原理与三角形相似知识的运用.通过相似三角形,来确定反射后的点的位置,从而可得反射的次数,由勾股定理来确定小球经过的路程,是一道学科综合试题,属于难题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
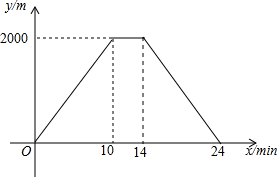 小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系.
小明骑自行车从甲地到乙地,到达乙地后,休息了一段时间,然后原路返回,停在甲地.整个过程保持匀速前进,设小明出发x(min)后,到达距离甲地y(m)的地方,图中的折线表示的是y与x之间的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 生产甲产品件数(件) | 生产乙产品件数(件) | 所用总时间(分) |
| 10 | 10 | 500 |
| 15 | 20 | 900 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
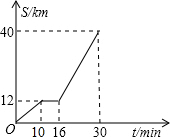 如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
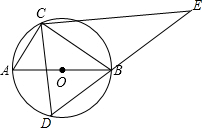 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
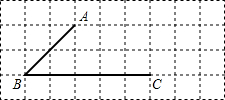
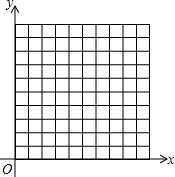 在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.
在平面直角坐标系中,设坐标的单位长度为1cm,点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题.| P从O出发的时间 | 可以得到的整点的坐标 | 可以得到的整点的个数 |
| 1秒 | (0,1)、(1,0) | 2个 |
| 2秒 | (2,0)、(0,2)、(1,1) | 3 |
| 3秒 | (3,0)、(0,3)、(1,2)、(2,1) | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com