
分析 ①原式提取公因式即可得到结果;
②原式利用十字相乘法分解即可;
③原式利用平方差公式分解即可;
④原式利用完全平方公式及平方差公式分解即可.
解答 解:①4m2n-8n2+2n=2n(2m2-4n+1);
②a2+9a-36=(a-3)(a+12);
③9(x+2y)2-4(x-y)2=[3(x+2y)+2(x-y)][3(x+2y)-2(x-y)]=(5x+4y)(x+8y);
④(x2-5)2+8(5-x2)+16=(x2-5)2-8(x2-5)+16=(x2-9)2=(x+3)2(x-3)2.
点评 此题考查了提公因式法与公式法的综合运用,以及因式分解-十字相乘法,熟练掌握因式分解的方法是解本题的关键.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:选择题
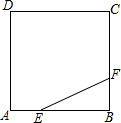 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
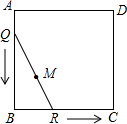 如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )
如图,正方形ABCD的边长为1,将长为1的线段QR的两端放在正方形相邻的两边上同时滑动.如果点Q从点A出发,按A→B→C→D→A的方向滑动到A停止,同时点R从点B出发,按B→C→D→A→B的方向滑动到B停止,在这个过程中,线段QR的中点M所经过的路线围成的图形面积为( )| A. | $\frac{π}{4}$ | B. | 4-π | C. | π | D. | $\frac{4-π}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
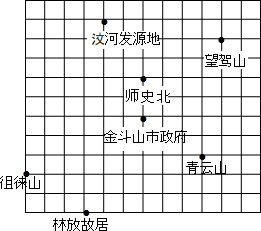 图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.
图中是某市旅游景点示意图,请建立适当的坐标系,使横轴与网格线的横线平行,纵轴与网格线的竖线平行,并且使青云山的坐标为(3,-2),然后再写出下列各景点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
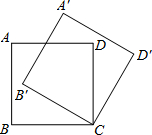 如图,将边长为6的正方形ABCD绕点C顺时针旋转30°得到正方形A′B′CD′,则点A的旋转路径长为$\sqrt{2}π$.(结果保留π)
如图,将边长为6的正方形ABCD绕点C顺时针旋转30°得到正方形A′B′CD′,则点A的旋转路径长为$\sqrt{2}π$.(结果保留π)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
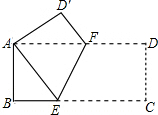 如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EC的长为( )
如图,在矩形ABCD中,AB=8,BC=16,将矩形ABCD沿EF折叠,使点C与点A重合,则折痕EC的长为( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com