
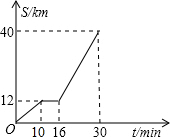
 如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:分析 (1)通过观察图象可以得出汽车前10分钟行驶的路程是12km,由速度=路程÷时间可以得出结论;
(2)由图象可以得出从第10分钟至16分钟汽车没有行驶,从而可以得出汽车停止的时间;
(3)首先假设该一次函数的解析式为S=mt+n.再根据当16≤t≤30时,关于S与t一次函数图象经过(16,12)、(30,40)两点,求得m、n的值,因而问题解决.
解答 解:(1)由图象得汽车在前10分钟内的平均速度是:
12÷10=1.2km/分钟;
(2)由图象得汽车在中途停止的时间为:
16-10=6分钟;
(3)设该一次函数的解析式为S=mt+n,
由图可知,图象经过点(16,12)和(30,40),因此可列如下方程组
$\left\{\begin{array}{l}{16m+n=12}\\{30m+n=40}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=2}\\{n=-20}\end{array}\right.$,
故所求的函数解析式为S=2t-20.
点评 本题考查了一次函数的应用,待定系数法求一次函数的解析式,准确识图并获取有用信息是解题的关键.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
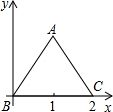 如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )
如图,边长为2的等边△ABC以点B为旋转中心,逆时针旋转60°时,点A的对应点的坐标( )| A. | (1,$\sqrt{3}$) | B. | (1,-$\sqrt{3}$) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )
如图,AB是半圆的直径,点O为圆心,点P沿OA→$\widehat{AB}$→BO匀速运动一周,设OP的长为s,运动时间为t,则s与t的函数关系图象大致是( )| A. | 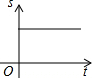 | B. | 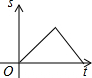 | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一个月内每天买进该晚报(份) | 150 | 200 |
| 当月利润(元) | 675 | 800 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
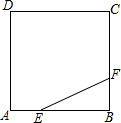 如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )
如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第n(n为正整数)次碰到点F时,小球P所经过的路程为( )| A. | $6\sqrt{5}n+5\sqrt{5}$ | B. | $5\sqrt{5}n+\sqrt{5}$ | C. | $6\sqrt{5}n-5\sqrt{5}$ | D. | $5\sqrt{5}n-4\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
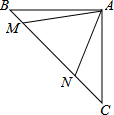 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.
如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
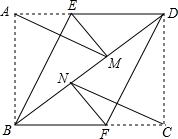 在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.
在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com