
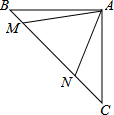
 如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$.
如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°.若BM=1,CN=3,则MN的长为$\sqrt{10}$. 分析 将△ABM逆时针旋转90°得到△ACF,连接NF,由条件可以得出△NCF为直角三角形,利用勾股定理就可以求出NF,通过证明三角形全等就可以MN=NF,求出NF即可.
解答 解:将△AMB逆时针旋转90°到△ACF,连接NF,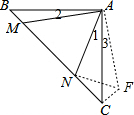
∴CF=BM,AF=AM,∠B=∠ACF.∠2=∠3,
∵△ABC是等腰直角三角形,AB=AC,
∴∠B=∠ACB=45°,∠BAC=90°,
∵∠MAN=45°,
∴∠NAF=∠1+∠3=∠1+∠2=90°-45°=45°=∠NAF,
在△MAN和△FAN中
$\left\{\begin{array}{l}{AN=AN}\\{∠MAN=∠FAN}\\{AM=AF}\end{array}\right.$
∴△MAN≌△FAN,
∴MN=NF,
∵∠ACF=∠B=45°,∠ACB=45°,
∴∠FCN=90°,
∵CF=BM=1,CN=3,
∴在Rt△CFN中,由勾股定理得:MN=NF=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
故答案为:$\sqrt{10}$.
点评 本题考查了旋转的性质的运用,勾股定理的运用,全等三角形的判定与性质,能正确作出辅助线是解此题的关键,难度适中.


科目:初中数学 来源: 题型:选择题
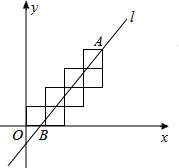 七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )
七个边长为1的正方形按如图所示的方式放置在平面直角坐标系xOy中,直线l经过点A(4,4)且将这七个正方形的面积分成相等的两部分,则直线l与x轴的交点B的横坐标为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
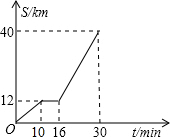 如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:
如图是某汽车行驶的路程S(千米)与时间t(分钟)的函数关系图.观察图中所提供的信息,解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.
(1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
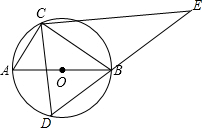 如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )
如图,AB是⊙O的直径,点C在⊙O上,且tan∠ABC=$\frac{1}{2}$,D是⊙O上的一个动点(C,D两点位于直径AB的两侧),连接CD,过点C作CE⊥CD交DB的延长线于点E.若⊙O的半径是$\sqrt{5}$,则线段CE长度的最大值是( )| A. | 2$\sqrt{5}$ | B. | 5$\sqrt{5}$ | C. | $\frac{16\sqrt{5}}{5}$ | D. | 4$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )
如图,△ABC中,∠C=90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ.在整个运动过程中,△MPQ的面积大小变化情况是( )| A. | 一直减小 | B. | 先减小后增大 | C. | 一直增大 | D. | 先增大后减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
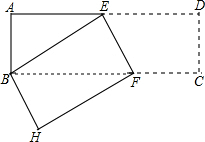 如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )
如图,将长方形纸片ABCD折叠,使点D与点B重合,折痕为EF.已知AB=6cm,BC=18cm,则Rt△ABE的面积为( )| A. | 27cm2 | B. | 24cm2 | C. | 22cm2 | D. | 20cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
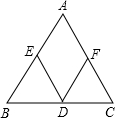 如图,在△ABC中,DE∥AC,DF∥AB.
如图,在△ABC中,DE∥AC,DF∥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com