
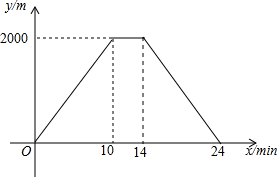
 С�������г��Ӽص��ҵأ������ҵغ���Ϣ��һ��ʱ�䣬Ȼ��ԭ·���أ�ͣ�ڼأ��������̱�������ǰ������С������x��min����������y��m���ĵط���ͼ�е����߱�ʾ����y��x֮��ĺ�����ϵ��
С�������г��Ӽص��ҵأ������ҵغ���Ϣ��һ��ʱ�䣬Ȼ��ԭ·���أ�ͣ�ڼأ��������̱�������ǰ������С������x��min����������y��m���ĵط���ͼ�е����߱�ʾ����y��x֮��ĺ�����ϵ������ ��1����y��x����ʽΪy=kx+b���ѣ�14��2000���루24��0���������k��b��ֵ������ȷ��������ʽ��
��2�����С����ҵ������õ�ʱ�䣬�������⻭��ͼ�Σ���ͼ��ʾ��
��3����С����صľ���y2��ʱ��x�Ĺ�ϵʽΪy2=px+q���ѣ�0��2000���루25��0���������p��q��ֵ��ȷ����y2��ʱ��x�Ľ���ʽ�������������40���г����̣�������̵Ľ⣬���鼴�ɵõ������
��� �⣺��1����y=kx+b��
�ѣ�14��2000���루24��0������ã�$\left\{\begin{array}{l}{14k+b=2000}\\{24k+b=0}\end{array}\right.$��
��ã�k=-200��b=4800��
��y=-200x+4800��
��2����������ã�С����ҵ������õ�ʱ��Ϊ2000��80=25��min��������ͼ�Σ���ͼ��ʾ��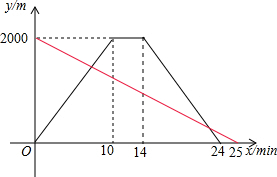
��3������С����صľ���y2��ʱ��x�Ĺ�ϵʽΪy2=px+q��
�ѣ�0��2000���루25��0������ã�$\left\{\begin{array}{l}{q=2000}\\{25p+q=0}\end{array}\right.$��
��ã�p=-80��q=2000��
��y2=-80x+2000��
��������ã�|-200x+4800+80x-2000|=40����-120x+2800=40��-120x+2800=-40��
��ã�x=23��x=$\frac{71}{3}$��
������$\frac{71}{3}$��23������14���������⣬
�ڵ�С������أ�С��δ��ʱ������-80t+2000=40����t=24.5��
��С����С�����14�����Ժ�����$\frac{71}{3}$���ӣ�24.5������23�������40�ף�
���� ���⿼����һ�κ�����Ӧ�ã�����ϵ������һ�κ�������ʽ����ͼ���ϵó����õ���Ϣ�ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
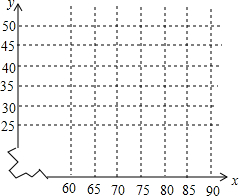 ij��˾�з���һ���²�Ʒ��ÿ���ɱ�50Ԫ���ù�˾������ij�ؽ��������ۣ��������ÿ����Ʒ�����۵���x��Ԫ�����Ʒ����������y������֮�����һ���Ĺ�ϵ�����±���ʾ��
ij��˾�з���һ���²�Ʒ��ÿ���ɱ�50Ԫ���ù�˾������ij�ؽ��������ۣ��������ÿ����Ʒ�����۵���x��Ԫ�����Ʒ����������y������֮�����һ���Ĺ�ϵ�����±���ʾ��| x��Ԫ�� | 60 | 65 | 70 | 75 | �� |
| y ������ | 40 | 35 | 30 | 25 | �� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У���ACB=90�㣬��CD���۵���CBD��ʹ��Bǡ������AC���ϵĵ�E��������A=22�㣬���BDC����67�㣮
��ͼ����ABC�У���ACB=90�㣬��CD���۵���CBD��ʹ��Bǡ������AC���ϵĵ�E��������A=22�㣬���BDC����67�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ��AB�ǰ�Բ��ֱ������OΪԲ�ģ���P��OA��$\widehat{AB}$��BO�����˶�һ�ܣ���OP�ij�Ϊs���˶�ʱ��Ϊt����s��t�ĺ�����ϵͼ������ǣ�������
��ͼ��AB�ǰ�Բ��ֱ������OΪԲ�ģ���P��OA��$\widehat{AB}$��BO�����˶�һ�ܣ���OP�ij�Ϊs���˶�ʱ��Ϊt����s��t�ĺ�����ϵͼ������ǣ�������| A�� | 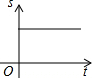 | B�� | 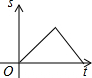 | C�� |  | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
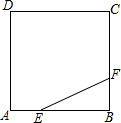 ��ͼ��������ABCD�ı߳�Ϊ3����E��F�ֱ��ڱ�AB��BC�ϣ�AE=BF=1��С��P�ӵ�E������ֱ�����F�˶���ÿ�����������εı�ʱ����������ʱ����ǵ�������ǣ���С��P��n��nΪ����������������Fʱ��С��P��������·��Ϊ��������
��ͼ��������ABCD�ı߳�Ϊ3����E��F�ֱ��ڱ�AB��BC�ϣ�AE=BF=1��С��P�ӵ�E������ֱ�����F�˶���ÿ�����������εı�ʱ����������ʱ����ǵ�������ǣ���С��P��n��nΪ����������������Fʱ��С��P��������·��Ϊ��������| A�� | $6\sqrt{5}n+5\sqrt{5}$ | B�� | $5\sqrt{5}n+\sqrt{5}$ | C�� | $6\sqrt{5}n-5\sqrt{5}$ | D�� | $5\sqrt{5}n-4\sqrt{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com