
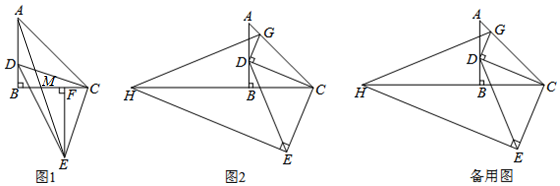
分析 (1)根据等腰直角三角形的性质得到CD=CE,再利用等角的余角相等得到∠DCB=∠CEF,然后根据“AAS”可证明△DBC≌△CFE;
(2)由△DBC≌△CFE得到BD=CF,BC=EF,再利用△ABC为等腰直角三角形得到AB=BC,所以AB=EF,AD=BF,接着证明△ABM≌△EFM,得到BM=FM,所以$\frac{AD}{BM}$=2;
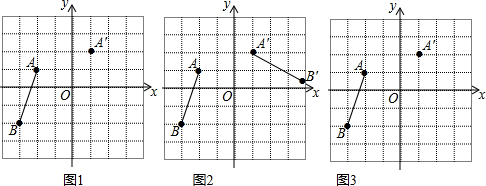
(3)在EH上截取EQ=DG,如图2,先证明△CDG≌△CEQ得到CG=CQ,∠DCG=∠ECQ,由于∠DCG+∠DCB=45°,则∠ECQ+∠DCB=45°,所以∠HCQ=45°,再证明△HCG≌△HCQ,则得到HG=HQ,然后可计算出$\frac{HE-GD}{GH}$=1.
解答 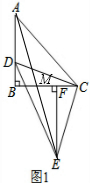 (1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
(1)证明:∵△CDE为等腰直角三角形,∠DCE=90°.
∴CD=CE,∠DCB+∠ECF=90°,
∵EF⊥BC,
∴∠ECF+∠CEF=90°,
∴∠DCB=∠CEF,
在△DBC和△CEF中,
$\left\{\begin{array}{l}{∠DBC=∠CFE}\\{∠DCB=∠CEF}\\{CD=EC}\end{array}\right.$,
∴△DBC≌△CFE;
(2)解:如图1,
∵△DBC≌△CFE,
∴BD=CF,BC=EF,
∵△ABC为等腰直角三角形,
∴AB=BC,
∴AB=EF,AD=BF,
在△ABM和△EFM中,
$\left\{\begin{array}{l}{∠AMB=∠EMF}\\{∠ABM=∠EFM}\\{AB=EF}\end{array}\right.$,
∴△ABM≌△EFM,
∴BM=FM,
∴BF=2BM,
∴AD=2BM,
∴$\frac{AD}{BM}$的值为2;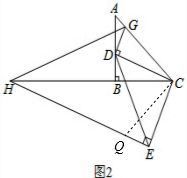 (3)解:$\frac{HE-GD}{GH}$的值不变.
(3)解:$\frac{HE-GD}{GH}$的值不变.
在EH上截取EQ=DG,如图2,
在△CDG和△CEQ中
$\left\{\begin{array}{l}{DG=EQ}\\{∠CDG=∠CEQ}\\{CD=CE}\end{array}\right.$,
∴△CDG≌△CEQ,
∴CG=CQ,∠DCG=∠ECQ,
∵∠DCG+∠DCB=45°,
∴∠ECQ+∠DCB=45°,
而∠DCE=90°,
∴∠HCQ=45°,
∴∠HCQ=∠HCG,
在△HCG和△HCQ中,
$\left\{\begin{array}{l}{HC=HC}\\{∠HCG=∠HCQ}\\{CG=CQ}\end{array}\right.$,
∴△HCG≌△HCQ,
∴HG=HQ,
∴$\frac{HE-GD}{GH}$=$\frac{HQ+QE-GD}{HG}$=$\frac{HG+DG-GD}{HG}$=1.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.也考查了等腰直角三角形的性质.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
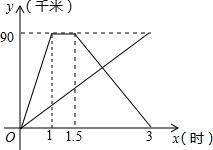 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
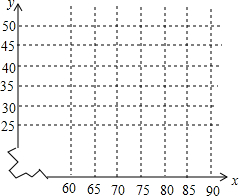 某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:
某公司研发出一种新产品,每件成本50元,该公司决定在某地进行试销售,结果发现每件产品的销售单价x(元)与产品的日销售量y(件)之间存在一定的关系,如下表所示:| x(元) | 60 | 65 | 70 | 75 | … |
| y (件) | 40 | 35 | 30 | 25 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com