
分析 (1)本题为分段函数,根据自变量的取值范围列出函数关系式即可;
(2)5千米应付多少元也就是当自变量x=5时代入满足自变量的函数式求出y的值即为所求;
(3)付车费19.8元,也就是函数式y=19.8代入求出相对应x的值.
解答 解:(1)由题意得,y=10+(x-4)×1.4,
=1.4x+4.4(x≥4);
(2)当x=5时,y=1.4×5+4.4=11.4(元),
答:某人乘坐出租车行驶5千米应付11.4元;
(3)y=19.8时,即1.4x+4.4=19.8,
解得:x=11.
答:若某人付了19.8元车费,那么出租车行驶了11km.
点评 本题考查的是用一次函数解决实际问题,关键看出是分段函数.然后根据题意给的已知的自变量或函数值求值.


科目:初中数学 来源: 题型:填空题
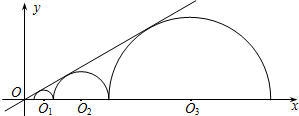 如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015=32014.
如图,圆心都在x轴正半轴上的半圆O1,半圆O2,…,半圆On与直线$y=\frac{{\sqrt{3}}}{3}x$相切,设半圆O1,半圆O2,…,半圆On的半径分别是r1,r2,…,rn,则当r1=1时,r2015=32014.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
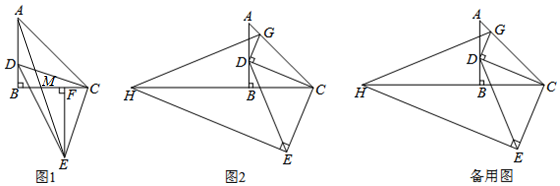
 如图,在△ABC中,
如图,在△ABC中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
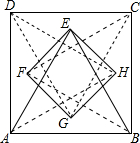 如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.
如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
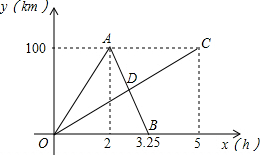 甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:
甲、乙两人分别从相距100km两地同时出发,相向而行.甲、乙两人距各自出发点的距离y(千米)与时间x(小时)之间的函数图象如图所示,其中折线OAB表示甲,线段OC表示乙.根据图象所提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com