
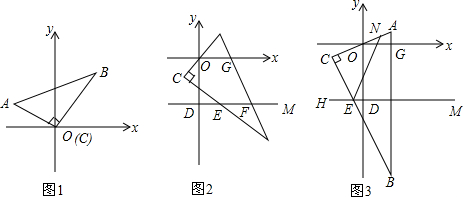
���� ��1������A��AM��x����M������B��BN��x����N�����ݡ�ABC�������������AMNB�������ȥ����ֱ�������ε������ʽ���㼴�ɵý⣻
��2�����ݶԶ�����Ⱥͻ�������ʵó���CED=40�㣬�ٸ����ڲ��ǵó���CEF=140�㼴�ɣ�
��3����CP��x�ᣬ��CP��DM��x�ᣬ����ƽ���ߵ����ʵá�AOG=��1����2+��CEF=180�㣬���ڡ�NED+��CEF=180�㣬���ԡ�2=��NED��Ȼ�����á�1+��2=90�㼴�ɵõ���AOG+��NEF=90��
��� �⣺��1����ͼ1������A��AM��x����M������B��BN��x����N��
��A��-3��a����B��3��b����
��AM=a��OM=3��BN=b��ON=3��
��MN=3+3=6��
��ABC�����=$\frac{1}{2}$��a+b����6-$\frac{1}{2}$��3a-$\frac{1}{2}$��3b��
=$\frac{1}{2}$��a+b����
��a+b-8=0��
��a+b=8
���ABC�����=$\frac{3}{2}$��8=12��
��2���ߡ�AOG=50�㣬
���POD=50�㣬
���COD=40�㣬
���CQO=50�㣬
���DQE=50�㣬
���CED=40�㣬
���CEF=140�㣻
��2��$\frac{��NEF}{��AOG}$Ϊ��ֵ���������£�
��CP��x�ᣬ��ͼ3��
��CP��DM��x�ᣬ
���AOG=��1����2+��CEF=180�㣬
����NED+��CEF=180�㣬
���2=��NED��
�ߡ�1+��2=90�㣬
���AOG+��NEF=90�㣬
�ߡ�NEF=��1+��CNP��
���NEF-��AOG=45��
��ɵã���NEF=67.5�㣬��AOG=22.5�㣬�ɵ�$\frac{��NEF}{��AOG}$=3���Ƕ�ֵ��
���� ���⿼����ƽ���ߵ��ж������ʣ�ƽ������ͬһ��ֱ�ߵ���ֱ��ƽ�У���ֱ��ƽ�У�ͬλ����ȣ���ֱ��ƽ�У�ͬ���ڽǻ�����


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪��ABC��
��֪��ABC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
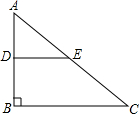 ��ͼ����Rt��ABC�У���B=90�㣬D��E�ֱ��DZ�AB��AC���е㣬DE=4�����ABC���ADE�������Ϊ4��1��
��ͼ����Rt��ABC�У���B=90�㣬D��E�ֱ��DZ�AB��AC���е㣬DE=4�����ABC���ADE�������Ϊ4��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com