
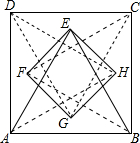
 如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$.
如图,分别以正方形ABCD的四条边为边,向其内部作等边三角形,得到△ABE、△BCF、△CDG、△DAH,连接EF、FG、GH、HE,若AB=2,则四边形EFGH的面积为8-4$\sqrt{3}$. 分析 先根据题意得出△ABE≌△BCF≌△CDG≌△DAH,连接EG并延长交CD于点M,交AB于点N,连接FH并延长交AD于点k,角BC于点l,
解答 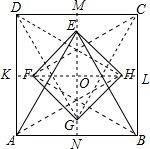 解:∵△ABE、△BCF、△CDG、△DAH均是以2为边长的等边三角形,
解:∵△ABE、△BCF、△CDG、△DAH均是以2为边长的等边三角形,
∴△ABE≌△BCF≌△CDG≌△DAH.
∵四边形ABCD是正方形,DG=CG,AE=BE,
∴点E线段AB的垂直平分线上,点G在CD的垂直平分线上,AB∥CD,
∴直线MN是线段CD与AB的垂直平分线.
∵AB=CD=2,
∴EN=$\sqrt{3}$,
∴ME=2-$\sqrt{3}$,
同理可得GN=2-$\sqrt{3}$,
∴EG=2-(2-$\sqrt{3}$-2-$\sqrt{3}$)=2$\sqrt{3}$-2.
同理可得,FH=2$\sqrt{3}$-2.
∵M、L、N、K分别是四边的中点,
∴EG⊥FH,且OG=OH,
∴四边形EFGH是正方形,
∴OG=OH=$\frac{1}{2}$EG=$\sqrt{3}$-1,
∴S四边形EFGH=GH2=OG2+OH2=($\sqrt{3}$-1)2+($\sqrt{3}$-1)2=8-4$\sqrt{3}$.
故答案为:8-4$\sqrt{3}$.
点评 本题考查的是全等三角形的判定与性质,熟知边长相等的等边三角形全等是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | -$\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知△ABC.
已知△ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
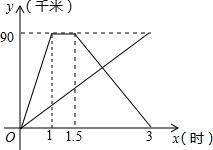 甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.
甲、乙两人同时从相距90千米的A地前往B地,甲乘汽车,乙骑电动车,甲到达B地停留半个小时后返回A地,如图是他们离A地的距离y(千米)与经过的时间x(小时)之间的函数关系图象.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,3) | B. | (2,-3) | C. | (-3,-2) | D. | (3,2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com