
【题目】如图,在平面直角坐标系![]() 中,点A的坐标为(5,0),点B的坐标为(3,2),直线
中,点A的坐标为(5,0),点B的坐标为(3,2),直线![]() 经过原点和点B,直线
经过原点和点B,直线![]() 经过点A和点B.
经过点A和点B.
(1)求直线![]() ,
, ![]() 的函数关系式;
的函数关系式;
(2)根据函数图像回答:不等式![]() 的解集为 ;
的解集为 ;
(3)若点![]() 是
是![]() 轴上的一动点,经过点P作直线
轴上的一动点,经过点P作直线![]() ∥
∥![]() 轴,交直线
轴,交直线![]() 于点C,交直线
于点C,交直线![]() 于点D,分别经过点C,D向
于点D,分别经过点C,D向![]() 轴作垂线,垂足分别为点E, F,得长方形CDFE.
轴作垂线,垂足分别为点E, F,得长方形CDFE.
①若设点P的横坐标为m,则点C的坐标为(m, ),点D的坐标为(m, );(用含字母m的式子表示)
②若长方形CDFE的周长为26,求m的值.

【答案】(1)直线![]() ,直线
,直线![]() ;(2)
;(2)![]() <0或
<0或![]() >5;(3)①
>5;(3)①![]() ,
, ![]() ;②
;②![]() 或
或![]() .
.
【解析】试题分析:
(1)把点A和B的坐标代入两函数的解析式列方程(组),解得k1、k2、b的值即可得到两函数的解析式;
(2)根据函数图象找到两个函数图象一个在![]() 轴上方,一个在
轴上方,一个在![]() 轴下方的时候所对应的自变量的取值范围即可得到不等式
轴下方的时候所对应的自变量的取值范围即可得到不等式![]() 的解集;
的解集;
(3)①由(1)中所求函数解析式即可得到点C和点D的纵坐标;②根据题意分![]() ,
, ![]() 和
和![]() 三种情况分别用含“m”的代数式表达出矩形CDEF的周长,结合矩形CDEF的周长为26即可求得对应的m的值.
三种情况分别用含“m”的代数式表达出矩形CDEF的周长,结合矩形CDEF的周长为26即可求得对应的m的值.
试题解析:
(1)把点B(3,2)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ;
;
把点A(5,0)和点B(3,2)代入![]() 得:
得: ![]() ,解得:
,解得: ![]() ,
,
∴![]() ,
, ![]() ;
;
(2)由图可知,当![]() 或
或![]() 时,两个函数的图象刚好一个在
时,两个函数的图象刚好一个在![]() 上方,一个在
上方,一个在![]() 轴的下方,
轴的下方,
∴不等式![]() 的解集为:
的解集为: ![]() 或
或![]() ;
;
(3)①∵点C在直线![]() 上,点D在直线
上,点D在直线![]() 上,且它们的横坐标为m,
上,且它们的横坐标为m,
∴点C、D的坐标分别为: ![]() 和
和![]() ;
;
②I、当m<0,
∵DC=EF=![]() ,DF=CE=-m,
,DF=CE=-m,
∴![]() 解得:m=-3;
解得:m=-3;
II、当![]() 时,同理可得:
时,同理可得: ![]() ,解得:
,解得: ![]() =-12(不合题意,舍去);
=-12(不合题意,舍去);
III、当![]() 时,同理可得:
时,同理可得: ![]() ,解得:
,解得: ![]() .
.
综上所述,m的值为![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高( )
A. 40% B. 33.4% C. 33.3% D. 30
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的平移得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请写出格点三角形DEF各顶点的坐标,并求出三角形DEF的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )



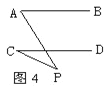
A. 、1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图,⊙O是△ABC的外接圆,圆心O在AB上,且∠B=2∠A,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,EF=FC.
(1)求证:CF是⊙O的切线;
(2)若⊙O的半径为2,且AC=CE,求AM的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:随着人们认识的不断深入,毕达哥拉斯学派逐渐承认![]() 不是有理数,并给出了证明.假设是
不是有理数,并给出了证明.假设是![]() 有理数,那么存在两个互质的正整数p,q,使得
有理数,那么存在两个互质的正整数p,q,使得![]() ,于是
,于是![]() ,两边平方得p2=2q2 . 因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2 , 即q2=2s2 , 所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明,
,两边平方得p2=2q2 . 因为2q2是偶数,所以p2是偶数,而只有偶数的平方才是偶数,所以p也是偶数.因此可设p=2s,代入上式,得4s2=2q2 , 即q2=2s2 , 所以q也是偶数,这样,p和q都是偶数,不互质,这与假设p,q互质矛盾,这个矛盾说明, ![]() 不能写成分数的形式,即
不能写成分数的形式,即![]() 不是有理数.请你有类似的方法,证明
不是有理数.请你有类似的方法,证明![]() 不是有理数.
不是有理数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com