练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．先化简，再求值
    [（$\sqrt{2}$xy+1）（$\sqrt{2}$xy-1）-（xy+1）2+3]÷（1-xy），其中x=10，y=5-1．

    分析 原式中括号中利用平方差公式，完全平方公式化简，合并后利用多项式除以单项式法则计算得到最简结果，把x与y的值代入计算即可求出值．

    解答 解：原式=（2x2y2-1-x2y2-2xy-1+3）÷（1-xy）=（x2y2-2xy+1）÷（1-xy）=（1-xy）2÷（1-xy）=1-xy，
    当x=10，y=5-1=$\frac{1}{5}$时，原式=1-2=-1．

    点评 此题考查了整式的混合运算-化简求值，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    19．（1）已知抛物线y=mx2+（3m-1）x-3与x轴交于两个不同的整数点，且m为正整数，试确定抛物线的解析式；
    （2）若点P（x1，k）与Q（x1+n，k）都在（1）中的抛物线上（点P，Q不重合），将抛物线在PQ下方的部分沿PQ翻折，抛物线的其它部分保持不变，得到一个新图象．当这个新图象与x轴恰好只有两个公共点时，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（-3，2），B（0，4），C（0，2）．
    （1）将△ABC向下平移4个单位长度，作出平移后的图形△A1B1C1，并写出A1的坐标（-3，-2）．
    （2）将△ABC以点C为旋转中心，顺时针方向旋转90°，作出旋转后的图形△A2B2C（不要求尺规作图，但要标出三角形各顶点字母）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

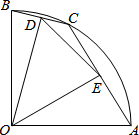    14．如图，在扇形OAB中，∠AOB=90°，点C是$\widehat{AB}$上的一个动点（不与A，B重合），OD⊥BC，OE⊥AC，垂足分别为D，E．若DE=1，则扇形OAB的面积为（　　）
    A．$\frac{π}{2}$B．$\frac{2}{3}π$C．πD．2π

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

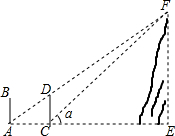    1．如图，相邻两输电杆AB、CD相距100m，高度都为20m，驾驶员开小汽车到A处时发现前方输电杆CD的顶部与山顶F恰好在一条直线上，小汽车沿平路往前开至C处时看到山顶F的仰角为α=42°，求山顶F的高．（精确到0.1m）
    （参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.90）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

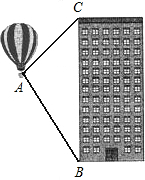    11．热气球的探测器显示，从热气球A处看一栋高楼顶部的仰角为45°，看这栋高楼底部的俯角为60°，这栋高楼的高是100米，A处与高楼的水平距离是50（$\sqrt{3}$-1）米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若将抛物线y=$\frac{1}{2}$x2先向左平移2个单位，再向下平移1个单位得到新的抛物线，则新抛物线的表达式是（　　）
    A．$y=\frac{1}{2}{（x+2）^2}-1$B．$y=\frac{1}{2}{（x-2）^2}-1$C．y=（x+2）2-1D．$y=\frac{1}{2}（x-2）+1$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．计算：（$\frac{1}{3}$）-1-|-5|$-\sqrt{9}$+（π-1）0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．若等腰三角形的周长是25cm，一腰上的中线把等腰三角形的周长分成两部分，且其中一部分与另一部分的差是4cm，求这个等腰三角形的底边长．

    查看答案和解析>>

    同步练习册答案