
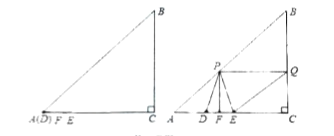
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC=10cm,长为4cm的线段DE在边AC上,且点D与点A重合,点F是DE的中点,线段DE从点A出发,沿AC方向向点C匀速运动,直到点E与点C重合,速度1cm/s。过点F作PF⊥AC,交AB于点P,过点P作PQ//AC,交BC于点Q,连接PD,PE,QE,设线段DE的运动时间为t(s).(0≤t≤6)
(1)请分别用含有t的代数式表示线段PF、BQ
(2)当t为何值时,四边形PFCQ为正方形?
(3)设四边形PDEQ的面积为y(cm)请求出y与t之间的函数关系式,并求出当t为何值时,四边形PDEQ的面积最大,最大是多少?
(4)是否存在某一时刻t,使得EP平分∠AEQ?若存在,求出此时t的值;若不存在,请说明理由.
【答案】(1)PF=t+2,BQ=8-t;(2)t=3s;(3)t=5,y=24.5;(4)存在.![]() 时,EP平分∠AEQ
时,EP平分∠AEQ
【解析】
(1)根据∠C=90°,AC=BC=10cm,可得∠A=![]() ,再根据PF⊥AC可得AF=PF,根据题意可得AF=t+2,CF=8-t,即可得出答案。
,再根据PF⊥AC可得AF=PF,根据题意可得AF=t+2,CF=8-t,即可得出答案。
(2)当PF=PQ时,四边形PFCQ为正方形,列出方程即可。
(3)用矩形DFCQ的面积加上三角形PDF的面积,再减去三角形QEC的面积得到四边形PDEQ的面积,列出y与t的函数关系式即可。
(4)先假设得EP平分∠AEQ,则∠AEP=∠QEP, 再根据 PQ//AC,得出∠AEP=∠QPE, ∠QEP=∠QPE,得出QE=QP,列出方程,方程有解就存在,没解就不存在。
(1)∵∠C=90°,AC=BC=10cm,∴∠A=∠B=![]() , ∵PF⊥AC,∴∠AFP=90°, ∴AF=PF,同理可证,BQ=PQ,∵点F是DE的中点,DE=4,∴DF=EF=2, ∴AF=t+2,∴PF=t+2,则CF=AC-AF=8-t,∵PF⊥AC,∠C=90°,PQ//AC,则四边形PFCQ是矩形,∴PQ=CF, BQ=CF = 8-t;
, ∵PF⊥AC,∴∠AFP=90°, ∴AF=PF,同理可证,BQ=PQ,∵点F是DE的中点,DE=4,∴DF=EF=2, ∴AF=t+2,∴PF=t+2,则CF=AC-AF=8-t,∵PF⊥AC,∠C=90°,PQ//AC,则四边形PFCQ是矩形,∴PQ=CF, BQ=CF = 8-t;
(2)∵四边形PFCQ为正方形,∴PF= CF,∴t+2=8-t,∴t=3,∴t=3时四边形PFCQ为正方形。
(3)y=![]() =(t+2)(8-t)+
=(t+2)(8-t)+![]() 2(t+2)-
2(t+2)-![]() (10-t-4)(t+2)
(10-t-4)(t+2)
∴y=-![]() +5t+12,∵a=-
+5t+12,∵a=-![]() 0,∴当t=5时,
0,∴当t=5时,![]() =24.5
=24.5
∴当t=5时,四边形PDEQ的面积最大,最大面积为24.5
(4)∵EP平分∠AEQ,∴∠AEP=∠QEP, ∵PQ//AC,∴∠AEP=∠QPE, ∴∠QEP=∠QPE, ∴QE=QP=8-t, ∴在Rt![]() ECQ中,
ECQ中,![]() ∴
∴![]()
解得:t=![]() ,t=
,t=![]() (舍去)
(舍去)
∴存在![]() 时,EP平分∠AEQ
时,EP平分∠AEQ


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:
【题目】如图⊙O的内接△ABC中,外角∠ACF的角平分线与⊙O相交于D点,DP⊥AC,垂足为P,DH⊥BF,垂足为H.问:
(1)∠PDC与∠HDC是否相等,为什么?
(2)图中有哪几组相等的线段?
(3)当△ABC满足什么条件时,△CPD∽△CBA,为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 0 |
| 2 |
| 0 | m | ﹣6 | ﹣ | … |
(1)求这个二次函数的表达式;
(2)求m的值;
(3)在给定的直角坐标系中,画出这个函数的图象;
(4)根据图象,写出当y<0时,x的取值范围.
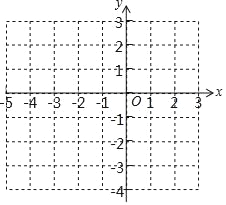
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C.抛物线
与x轴交于点A,与y轴交于点C.抛物线![]() 经过A,C两点,且与x轴交于另一点B(点B在点A右侧).
经过A,C两点,且与x轴交于另一点B(点B在点A右侧).

(1)求抛物线的解析式及点B坐标;
(2)若点M是线段BC上的一动点,过点M的直线EF平行y轴交x轴于点F,交抛物线于点E.求ME长的最大值;
(3)试探究当ME取最大值时,在抛物线上、x轴下方是否存在点P,使以M,F,B,P为顶点的四边形是平行四边形?若存在,请求出点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试航任务.某日航母在南海海域试航,如图,海中有一个小岛A,并测得该岛四周10海里内有暗礁,航母由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处,之后如果航母继续向东航行,途中会有触礁的危险吗?(参考数据:sin55°=0.8,cos55°=0.6,tan55°=1.4,sin25°=0.4,cos25°=0.9,tan25°=0.5)
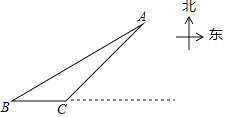
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在相同条件下各射靶10次,每次射靶的成绩情况如图所示:
(1)请填写下表:
平均数 | 方差 | 中位数 | 命中9环以上(包括9环)次数 | |
甲 | 7 |
|
|
|
乙 |
| 5.4 |
|
|
(2)请你就下列两个不同的角度对这次测试结果进行
①从平均数和方差相结合看(分析谁的成绩更稳定);
②从平均数和命中9环(包括9环)以上次数相结合看(分析谁的潜能更大).
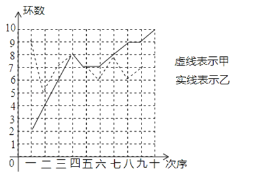
查看答案和解析>>
科目:初中数学 来源: 题型:
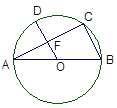
【题目】如图,A,B,C三点在⊙O上,且AB是⊙O的直径,半径OD⊥AC,垂足为F,若∠A=30,OF=3,则OA=_____,AC=_____,BC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场试销一种成本为每件![]() 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于
元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于![]() ,经试销发现,销售量
,经试销发现,销售量![]() (件)与销售单价
(件)与销售单价![]() (元)符合一次函数
(元)符合一次函数![]() ,且
,且![]() 时,
时,![]() ;
;![]() 时,
时,![]() .
.
![]() 求一次函数
求一次函数![]() 的表达式;
的表达式;
![]() 若该商场获得利润为
若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
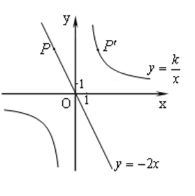
【题目】如图,已知直线y=-2x经过点P(-2,m),点P关于y轴的对称点P′在反比例函数![]() (
(![]() )的图象上.
)的图象上.
(1)求m的值;
(2)直接写出点P′的坐标;
(3)求反比例函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com