
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,AB=25,BC=15.
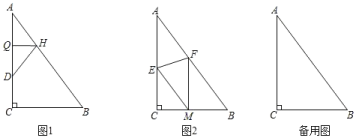
(1)如图1,折叠△ABC使点A落在AC边上的点D处,折痕交AC、AB分别于Q、H,若![]() ,则HQ= .
,则HQ= .
(2)如图2,折叠△ABC使点A落在BC边上的点M处,折痕交AC、AB分别于E、F.若FM∥A,求证:四边形AEMF是菱形;
(3)在(1)(2)的条件下,线段CQ上是否存在点P,使得△CMP和△HQP相似?若存在,求出PQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
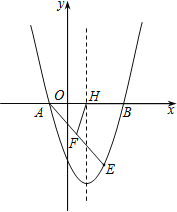
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
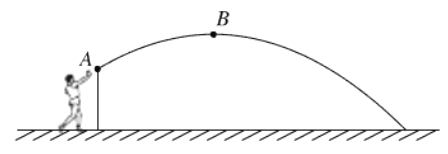
【题目】为了在校运会中取得更好的成绩,小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是![]() 米,当铅球运行的水平距离为3米时,达到最大高度
米,当铅球运行的水平距离为3米时,达到最大高度![]() 的B处.小丁此次投掷的成绩是多少米?
的B处.小丁此次投掷的成绩是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
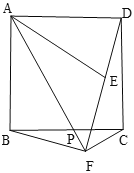
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
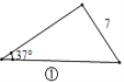
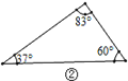
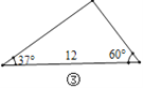
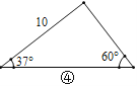
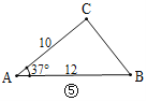
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
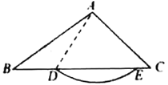
【题目】在![]() 中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称
中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称![]() 为
为![]() 的A-外截弧.例如,图中
的A-外截弧.例如,图中![]() 是
是![]() 的一条A-外截弧.在平面直角坐标系xOy中,已知
的一条A-外截弧.在平面直角坐标系xOy中,已知![]() 存在A-外截弧,其中点A的坐标为
存在A-外截弧,其中点A的坐标为![]() ,点B与坐标原点O重合.
,点B与坐标原点O重合.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,满足条件的点C是_______.
中,满足条件的点C是_______.
(2)若点C在直线![]() 上.
上.
①求点C的纵坐标的取值范围.
②直接写出![]() 的A-外截弧所在圆的半径r的取值范围.
的A-外截弧所在圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=10,BC=8,以CD为直径作⊙O.将矩形ABCD绕点C旋转,使所得矩形A′B′CD′的边A′B′与⊙O相切,切点为E,则A′E的长为( )

A. 8 B. 7 C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】例:利用函数图象求方程x2﹣2x﹣2=0的实数根(结果保留小数点后一位).
解:画出函数y=x2﹣2x﹣2的图象,它与x轴的公共点的横坐标大约是﹣0.7,2.7.所以方程x2﹣2x﹣2=0的实数根为x1≈﹣0.7,x2≈2.7.我们还可以通过不断缩小根所在的范围估计一元二次方程的根.……这种求根的近似值的方法也适用于更高次的一元方程.
根据你对上面教材内容的阅读与理解,解决下列问题:
(1)利用函数图象确定不等式x2﹣4x+3<0的解集是 ;利用函数图象确定方程x2﹣4x+3=![]() 的解是 .
的解是 .
(2)为讨论关于x的方程|x2﹣4x+3|=m解的情况,我们可利用函数y=|x2﹣4x+3|的图象进行研究.
①请在网格内画出函数y=|x2﹣4x+3|的图象;
②若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解,则m的取值范围为 ;
③若关于x的方程|x2﹣4x+3|=m有四个不相等的实数解x1,x2,x3,x4(x1<x2<x3<x4),满足x4﹣x3=x3﹣x2=x2﹣x1,求m的值.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com