
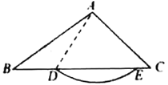
【题目】在![]() 中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称
中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称![]() 为
为![]() 的A-外截弧.例如,图中
的A-外截弧.例如,图中![]() 是
是![]() 的一条A-外截弧.在平面直角坐标系xOy中,已知
的一条A-外截弧.在平面直角坐标系xOy中,已知![]() 存在A-外截弧,其中点A的坐标为
存在A-外截弧,其中点A的坐标为![]() ,点B与坐标原点O重合.
,点B与坐标原点O重合.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,满足条件的点C是_______.
中,满足条件的点C是_______.
(2)若点C在直线![]() 上.
上.
①求点C的纵坐标的取值范围.
②直接写出![]() 的A-外截弧所在圆的半径r的取值范围.
的A-外截弧所在圆的半径r的取值范围.
【答案】(1)C2、C3;(2)-2<y<![]() 或y>2;(3)
或y>2;(3)![]() <r<5或
<r<5或![]() <r<5.
<r<5.
【解析】
(1)如图,根据BC1⊥AB可得△ABC1没有A-外截弧,作AF⊥BC2于F,由AC2<AB可得当AF<AD2<AC2时,△ABC2有A-外截弧;作AG⊥BC3于G,根据点C3坐标,可求出AC3的长,可得AC3<AB,即可得出AG<AD1<AC3时,△ABC3有A-外截弧;根据A、B、C4坐标可求出BC4、AC4的长,根据勾股定理逆定理可得△ABC4是直角三角形,且AC4⊥BC4,可得△ABC4没有A-外截弧,综上即可得答案;
(2)①根据△ABC有A-外截弧可得∠ABC<90°,可得x>0,设点C坐标为(m,m-2),利用直角三角形斜边中线的性质可求出∠ACB=90°时点C的坐标,根据∠ACB<90°时,△ABC有A-外截弧可得m的取值范围,代入y=x-2,即可得点C纵坐标的取值范围;
②求出∠ACB=90°时AC的长,进而可得答案.
(1)如图,∵BC1⊥AB,
∴△ABC1没有A-外截弧,
作AF⊥BC2于F,
∵A(5,0),B(0,0),C2(5,-3),
∴∠BAC2=90°,AC2=3,AB=5,
∴AC2<AB,
∴AF<AD2<AC2时,△ABC2有A-外截弧,满足条件,
作AG⊥BC3于G,
∵C3(6,4),
∴AC3=![]() <AB,
<AB,
∴AG<AD1<![]() 时,△ABC3有A-外截弧,满足条件,
时,△ABC3有A-外截弧,满足条件,
∵C4(4,2),
∴BC4=![]() ,AC4=
,AC4=![]() ,AB=5,
,AB=5,
∵(![]() )2+(
)2+(![]() )2=52,
)2=52,
∴△ABC4是直角三角形,∠AC4B=90°,
∴△ABC4没有A-外截弧,
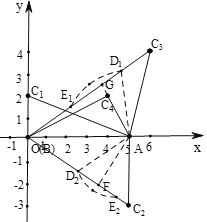
综上所述:满足条件的点C是C2、C3.
故答案为:C2、C3
(2)①∵点C在直线y=x-2上,
∴设点C的坐标为(m,m-2),
∵△ABC有A-外截弧,
∴∠ABC<90°,
∴m>0,
当∠ACB=90°时,
∵A(5,0),B(0,0),
∴斜边AB的中点H的坐标为(2.5,0),
∴(m-2.5)2+(m-2)2=(2.5)2,
解得:m1=![]() ,m2=4,
,m2=4,
∴∠ACB=90°时,点C坐标为(![]() ,
,![]() )或(4,2),
)或(4,2),
∵直线解析式为y=x-2,
∴x=0时,y=-2,
∴与y轴交点为(0,-2),
∵△ABC有A-外截弧时,∠ACB<90°,
∴点C的纵坐标的取值范围为-2<y<![]() 或y>2.
或y>2.
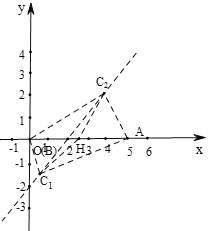
②由①得x=![]() 或x=4时,∠ACB=90°,
或x=4时,∠ACB=90°,
∴C1(![]() ,
,![]() ),C2(4,2),
),C2(4,2),
∴AC1=![]() ,AC2=
,AC2=![]() ,
,
∴![]() 的A-外截弧所在圆的半径r的取值范围为:
的A-外截弧所在圆的半径r的取值范围为:![]() <r<5或
<r<5或![]() <r<5.
<r<5.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
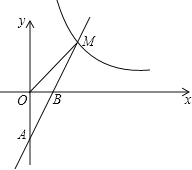
【题目】如图,一次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,与反比例函数
两点,与反比例函数![]() 的图象在第一象限内的交点为
的图象在第一象限内的交点为![]() .
.
![]() 求一次函数和反比例函数的表达式;
求一次函数和反比例函数的表达式;
![]() 在x轴上是否存在点P,使
在x轴上是否存在点P,使![]() ?若存在,求出点P的坐标;若不存在,说明理由.
?若存在,求出点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
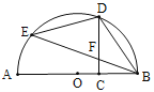
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 上部分点的横坐标x与纵坐标y的对应值如下表
上部分点的横坐标x与纵坐标y的对应值如下表
x | … | -2 | -1 | 0 | 1 | 2 | 3 | … |
y | … | -4 | 0 | 2 | 2 | 0 | -4 | … |
下列结论:①抛物线开口向下;②当![]() 时,y随x的增大而减小;③抛物线的对称轴是直线
时,y随x的增大而减小;③抛物线的对称轴是直线![]() ;④函数
;④函数![]() 的最大值为2.其中所有正确的结论为( )
的最大值为2.其中所有正确的结论为( )
A.①②③B.①③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B是![]() 的半径OA上的一点(不与端点重合),过点B作OA的垂线交
的半径OA上的一点(不与端点重合),过点B作OA的垂线交![]() 于点C,D,连接OD,E是
于点C,D,连接OD,E是![]() 上一点,
上一点,![]() ,过点C作
,过点C作![]() 的切线l,连接OE并延长交直线l于点F.
的切线l,连接OE并延长交直线l于点F.
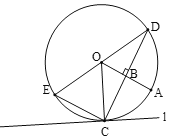
(1)①依题意补全图形.
②求证:∠OFC=∠ODC.
(2)连接FB,若B是OA的中点,![]() 的半径是4,求FB的长.
的半径是4,求FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
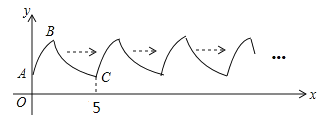
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
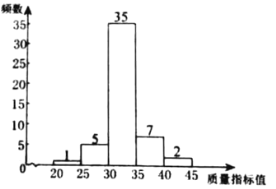
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径.
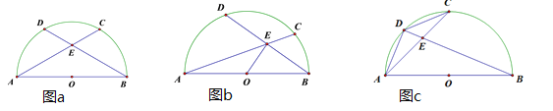
(1)如图a,点D为![]() 的中点,当弦BD=AC时,求∠A.
的中点,当弦BD=AC时,求∠A.
(2)如图b,点D为![]() 的中点,当AB=6,点E为BD的中点时,求OE的长.
的中点,当AB=6,点E为BD的中点时,求OE的长.
(3)如图c,点D为![]() 上任意一点(不与A、C重合),若点C为
上任意一点(不与A、C重合),若点C为![]() 的中点,探求BD、AD、CD之间的数量关系,直接写出你探求的结论,不要求证明.
的中点,探求BD、AD、CD之间的数量关系,直接写出你探求的结论,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,半径OC=6,D是半径OC上一点,且 OD=4.A,B是⊙O上的两个动点,∠ADB=90°,F是AB的中点,则OF的长的最大值等于______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com