
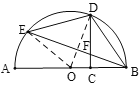
【题目】如图,AB是⊙O的直径,C是线段OB上的一点(不与点B重合),D,E是半圆上的点且CD与BE交于点F,用①![]() ,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
,②DC⊥AB,③FB=FD中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
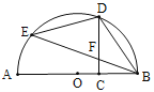
A.0B.1C.2D.3
【答案】D
【解析】
连接OE、OD,
(1)当![]() ,DC⊥AB时,由圆周角定理可得∠EOD=∠DOB,根据等腰三角形的性质可得OF⊥BE,由CD⊥AB可得∠OFB=∠OCD=90°,利用AAS可证明△OCD≌OFB,可得∠ODC=∠OBF,根据等腰三角形的性质可得∠OBD=∠ODB,利用角的和差关系可得∠FBD=∠FDB,即可证明FB=FD;
,DC⊥AB时,由圆周角定理可得∠EOD=∠DOB,根据等腰三角形的性质可得OF⊥BE,由CD⊥AB可得∠OFB=∠OCD=90°,利用AAS可证明△OCD≌OFB,可得∠ODC=∠OBF,根据等腰三角形的性质可得∠OBD=∠ODB,利用角的和差关系可得∠FBD=∠FDB,即可证明FB=FD;
(2)当![]() ,FB=FD时,同(1)可得OF⊥BE,根据等腰三角形的性质可得∠OBD=∠ODB,∠FBD=∠FDB,利用角的和差关系可得∠ODC=∠OBF,利用ASA可证明△OCD≌OFB,可得∠OFB=∠OCD=90°,可得DC⊥AB;
,FB=FD时,同(1)可得OF⊥BE,根据等腰三角形的性质可得∠OBD=∠ODB,∠FBD=∠FDB,利用角的和差关系可得∠ODC=∠OBF,利用ASA可证明△OCD≌OFB,可得∠OFB=∠OCD=90°,可得DC⊥AB;
(3)当DC⊥AB,FB=FD时,同(2)可得△OCD≌OFB,由DC⊥AB可得∠OFB=∠OCD=90°,根据垂径定理可得![]() ,综上即可得答案.
,综上即可得答案.
如图,连接OE、OD,
(1)当![]() ,DC⊥AB时,
,DC⊥AB时,
∵![]() ,OD为半径,
,OD为半径,
∴∠EOD=∠DOB,
∵OE=OB,
∴OF⊥BE,
∴∠OFB=90°,
∵DC⊥AB,
∴∠DCB=∠OFB=90°,
在△OCD和△OFB中,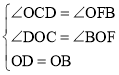 ,
,
∴△OCD≌△OFB,
∴∠ODC=∠OBF,
∵OD=OB,
∴∠ODB=∠OBD,
∴∠OBD-∠OBF=∠ODB-∠ODC,即∠FDB=∠FBD,
∴FB=FD.
(2)当![]() ,FB=FD时,
,FB=FD时,
∵![]() ,OD为半径,
,OD为半径,
∴∠EOD=∠DOB,
∵OE=OB,
∴OF⊥BE,
∴∠OFB=90°,
∵OD=OB,FB=FD,
∴∠ODB=∠OBD,∠FDB=∠FBD,
∴∠ODC=∠OBF,
在△OCD和△OFB中,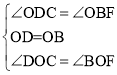 ,
,
∴△OCD≌△OFB,
∴∠OCD=∠OFB=90°,
∴DC⊥AB.
(3)当DC⊥AB,FB=FD时,
∵DC⊥AB,
∴∠OCD=90°,
∵OD=OB,FB=FD,
∴∠ODB=∠OBD,∠FDB=∠FBD,
∴∠ODC=∠OBF,
在△OCD和△OFB中,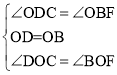 ,
,
∴△OCD≌△OFB,
∴∠OFB=∠OCD=90°,
∴OD⊥BE,
∵OD是半径,
∴![]() .
.
综上所述,组成真命题的个数为3,
故选:D.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
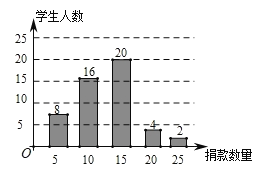
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
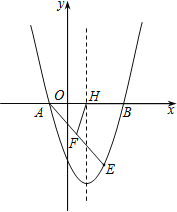
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
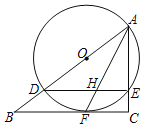
【题目】如图,在Rt△ABC中,∠C=90°,点D是AB上一点,以AD为直径作⊙O交AC于E,与BC相切于点F,连接AF.
(1)求证:∠BAF=∠CAF;
(2)若AC=3,BC=4,求BD和CE的长;
(3)在(2)的条件下,若AF与DE交于H,求FHFA的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
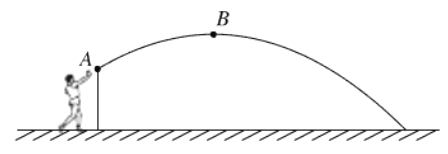
【题目】为了在校运会中取得更好的成绩,小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是![]() 米,当铅球运行的水平距离为3米时,达到最大高度
米,当铅球运行的水平距离为3米时,达到最大高度![]() 的B处.小丁此次投掷的成绩是多少米?
的B处.小丁此次投掷的成绩是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,P是边BC上的一动点(不与点B,C重合),点B关于直线AP的对称点为E,连接AE,连接DE并延长交射线AP于点F,连接BF
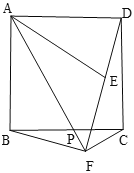
(1)若![]() ,直接写出
,直接写出![]() 的大小(用含
的大小(用含![]() 的式子表示).
的式子表示).
(2)求证:![]() .
.
(3)连接CF,用等式表示线段AF,BF,CF之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
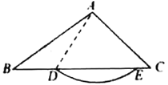
【题目】在![]() 中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称
中,D是边BC上一点,以点A为圆心,AD长为半径作弧,如果与边BC有交点E(不与点D重合),那么称![]() 为
为![]() 的A-外截弧.例如,图中
的A-外截弧.例如,图中![]() 是
是![]() 的一条A-外截弧.在平面直角坐标系xOy中,已知
的一条A-外截弧.在平面直角坐标系xOy中,已知![]() 存在A-外截弧,其中点A的坐标为
存在A-外截弧,其中点A的坐标为![]() ,点B与坐标原点O重合.
,点B与坐标原点O重合.
(1)在点![]() ,
,![]() ,
,![]() ,
,![]() 中,满足条件的点C是_______.
中,满足条件的点C是_______.
(2)若点C在直线![]() 上.
上.
①求点C的纵坐标的取值范围.
②直接写出![]() 的A-外截弧所在圆的半径r的取值范围.
的A-外截弧所在圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接国庆节,某商店购进了一批成本为每件30元的纪念商品.经调查发现,该商品每天的销售量![]() (件
(件![]() 与销售单价
与销售单价![]() (元
(元![]() 满足一次函数关系,其图象如图所示.
满足一次函数关系,其图象如图所示.

(1)求该商品每天的销售量![]() 与销售单价
与销售单价![]() 的函数关系式;
的函数关系式;
(2)若商店按不低于成本价,且不高于60元的单价销售,则销售单价定为多少,才能使销售该商品每天获得的利润![]() (元
(元![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com