
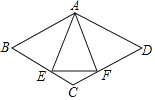
【题目】如图,在菱形ABCD中,点E,F分别在BC,CD上,且CE=CF,
(1)求证△ABE≌△ADF.
(2)若∠B=50°,AE⊥BC,求∠AEF的度数.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
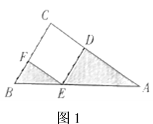
【题目】问题背景:如图1,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
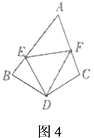
,四边形![]() 是正方形,求图中阴影部分的面积.
是正方形,求图中阴影部分的面积.
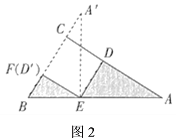
(1)发现:如图![]() ,小芳发现,只要将
,小芳发现,只要将![]() 绕点
绕点![]() 逆时针旋转一定的角度到达
逆时针旋转一定的角度到达![]() ,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为______;(直接写出答案)
,就能将阴影部分转化到一个三角形里,从而轻松解答.根据小芳的发现,可求出图1中阴影部分的面积为______;(直接写出答案)
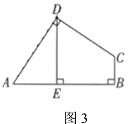
(2)应用:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 的长;
的长;
(3)拓展:如图![]() ,在四边形
,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以
,以![]() 为顶点作
为顶点作![]() 为
为![]() 角,角的两边分别交
角,角的两边分别交![]() ,
,![]() 于
于![]() ,
,![]() 两点,连接
两点,连接![]() ,请直接写出线段
,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系.
之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中,点![]() ,以线段
,以线段![]() 为直径作圆,圆心为
为直径作圆,圆心为![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:直线![]() 是
是![]() 的切线;
的切线;
(2)点![]() 为
为![]() 轴上任意一动点,连接
轴上任意一动点,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() :
:
①当![]() 时,求所有
时,求所有![]() 点的坐标 (直接写出);
点的坐标 (直接写出);
②求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市抽奖规则如下:在一个不透明的盒子里装有分别标有数字1、2、3、4的4个小球,它们的形状、大小、质地完全相同,顾客先从盒子里随机取出一个小球,记下小球上标有的数字,然后把小球放回盒子并搅拌均匀,再从盒子中随机取出一个小球,记下小球上标有的数字,并计算两次记下的数字之和若两次所得的数字之和为8,则可获得50元代金券一张:若所得的数字之和为6,则可获得30元代金券一张;若所得的数字之和为5,则可获得15元代金券一张:其他情况都不中奖.
(1)请用列表或树状图的方法,把抽奖一次可能出现的结果表示出来;
(2)假如你参加了该超市开业当天的一次抽奖活动,求能中奖的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
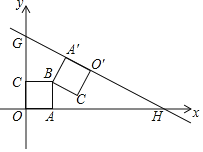
【题目】如图,直线y=![]() x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
A.4![]() B.
B.![]() C.5D.6
C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点I是△ABC的内心,∠AIC=124°,点E在AD的延长线上,则∠CDE的度数为( )
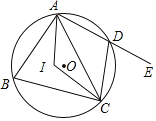
A. 56° B. 62° C. 68° D. 78°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( )
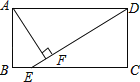
A. △AFD≌△DCE B. AF=![]() AD C. AB=AF D. BE=AD﹣DF
AD C. AB=AF D. BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
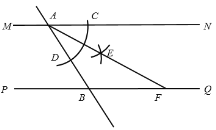
【题目】如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() .小亮同学利用尺规按以下步骤作图:①以点
.小亮同学利用尺规按以下步骤作图:①以点![]() 为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ;②分别以
;②分别以![]() 、
、![]() 为圆心,以大于
为圆心,以大于![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③做射线
;③做射线![]() 交
交![]() 于点
于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的内切圆半径长等于__________.
的内切圆半径长等于__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2﹣8x+16﹣m2=0(m≠0)是关于x的一元二次方程
(1)证明:此方程总有两个不相等的实数根;
(2)若等腰△ABC的一边长a=6,另两边长b、c是该方程的两个实数根,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com