
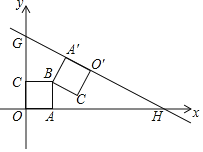
【题目】如图,直线y=![]() x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
x+b(b>2)与x轴,y轴分别交于H,G两点,边长为2的正方形OABC的边OA,OC分别在x轴,y轴上,点B在第一象限,正方形OABC绕点B逆时针旋转,OA的对应边O'A'恰好落在直线GH上,则b的值为( )
A.4![]() B.
B.![]() C.5D.6
C.5D.6
【答案】C
【解析】
过点A′作A′M⊥x轴,交CB的延长线与M,交x轴于D;可以证明∠BA′M=∠H,在Rt△A′BM中,A′B=2,tan∠BA′M=![]() ,分别求出BM=
,分别求出BM=![]() ,A′M=
,A′M=![]() ,确定A′的坐标为A′(
,确定A′的坐标为A′(![]() ,
,![]() ),再将点A′(
),再将点A′(![]() ,
,![]() )代入y=
)代入y=![]() x+b,即可求解.
x+b,即可求解.![]()
解:过点A′作A′M⊥x轴,交CB的延长线与M,交x轴于D,
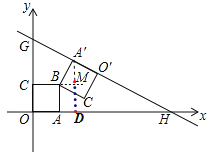
∵∠BA′M+∠MA′O′=90°,∠H+∠HA′M=90°,
∴∠BA′M=∠OHG,
∵y=![]() x+b,
x+b,
∴tan∠BA′M=tan∠OHG=![]() ,
,
设BM=5m,A′M=12m,
∵A′B=2,
∴(5m)2+(12m)2=4,
∴m=![]() ,
,
∴BM=![]() ,A′M=
,A′M=![]() ,
,
∵B(2,2),
∴A′(![]() ,
,![]() ),
),
将点A′(![]() ,
,![]() )代入y=
)代入y=![]() x+b,得
x+b,得
![]() ×
×![]() +b=
+b=![]() ,
,
∴b=5;
故选:C.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,点E在边
中,点E在边![]() 上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边
上,将点E绕点D逆时针旋转得到点F,若点F恰好落在边![]() 的延长线上,连接
的延长线上,连接![]() ,
,![]() ,
,![]() .
.
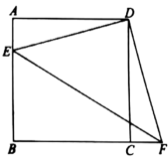
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,则
,则![]() 的面积为________.
的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小华同学设计的“作三角形的高线”的尺规作图的过程.
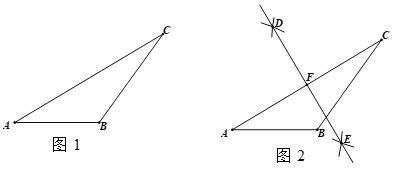
已知:如图1,△ABC.
求作:AB边上的高线.
作法:如图2,
①分别以A,C为圆心,大于![]() 长
长
为半径作弧,两弧分别交于点D,E;
② 作直线DE,交AC于点F;
③ 以点F为圆心,FA长为半径作圆,交AB的延长线于点M;
④ 连接CM.
则CM 为所求AB边上的高线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接DA,DC,EA,EC,
∵由作图可知DA=DC =EA=EC,
∴DE是线段AC的垂直平分线.
∴FA=FC .
∴AC是⊙F的直径.
∴∠AMC=______°(___________________________________)(填依据),
∴CM⊥AB.
即CM就是AB边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真阅读下面的数学小探究,完成所提出的问题
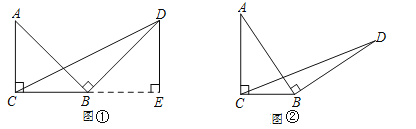
(1)探究1,如图①,在等腰直角三角形ABC中,∠ACB=90°,BC=3,将边 AB绕点B顺时针旋转90°得到线段BD,连接CD,过点D作BC边上的高DE,则DE与BC的数量关系是 . △BCD的面积为 .
(2)探究2,如图②,在一般的Rt△ABC中,∠ACB=90°,BC=![]() ,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含
,将边AB绕点B顺时针旋转90°得到线段BD,连接CD,请用含![]() 的式子表示△BCD的面积,并说明理由.
的式子表示△BCD的面积,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
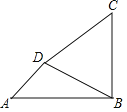
【题目】如图,海中有两个小岛![]() ,
,![]() ,某渔船在海中的
,某渔船在海中的![]() 处测得小岛D位于东北方向上,且相距
处测得小岛D位于东北方向上,且相距![]() ,该渔船自西向东航行一段时间到达点
,该渔船自西向东航行一段时间到达点![]() 处,此时测得小岛
处,此时测得小岛![]() 恰好在点
恰好在点![]() 的正北方向上,且相距
的正北方向上,且相距![]() ,又测得点
,又测得点![]() 与小岛
与小岛![]() 相距
相距![]() .
.
(1)求![]() 的值;
的值;
(2)求小岛![]() ,
,![]() 之间的距离(计算过程中的数据不取近似值).
之间的距离(计算过程中的数据不取近似值).
查看答案和解析>>
科目:初中数学 来源: 题型:
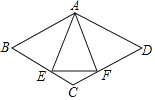
【题目】如图,在菱形ABCD中,点E,F分别在BC,CD上,且CE=CF,
(1)求证△ABE≌△ADF.
(2)若∠B=50°,AE⊥BC,求∠AEF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
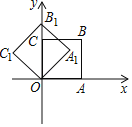
【题目】如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1,依此方式,绕点O连续旋转2018次得到正方形OA2018B2018C2018,如果点A的坐标为(1,0),那么点B2018的坐标为( )
A. (1,1) B. (0,![]() ) C. (
) C. (![]() ) D. (﹣1,1)
) D. (﹣1,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数![]() 的图象的一个分支.
的图象的一个分支.
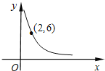
![]() 比例系数
比例系数![]() 的值是________;
的值是________;
![]() 写出该图象的另一个分支上的
写出该图象的另一个分支上的![]() 个点的坐标:________、________;
个点的坐标:________、________;
![]() 当
当![]() 在什么范围取值时,
在什么范围取值时,![]() 是小于
是小于![]() 的正数?
的正数?
![]() 如果自变量
如果自变量![]() 取值范围为
取值范围为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
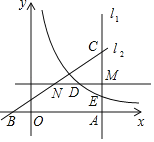
【题目】如图,直线l1经过点A(6,0),且垂直于x轴,直线l2:y=kx+b(b>0)经过点B(﹣2,0),与l1交于点C,S△ABC=16.点M是线段AC上一点,直线MN∥x轴,交l2于点N,D是MN的中点.双曲线y=![]() (x>0)经过点D,与l1交于点E.
(x>0)经过点D,与l1交于点E.
(1)求l2的解析式;
(2)当点M是AC中点时,求点E的坐标;
(3)当MD=1时,求m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com