练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知x，y，z是三个非负数，并且满足x+2y-5z=6，2x+y+5z=9．设k=3x+y+5z，记a为k的最大值，b为k的最小值，试求ab的值．

    【答案】117

    【解析】

    首先把x+2y-5z=6，2x+y+5z=9，组成方程组，分别用含z的代数式表示x和y，根据x，y，z是三个非负数求出z的取值范围，再把x和y代入k=3x+y+5z中，可得到k=-5z+13，求出k的最大值和最小值，即可以得到答案．

    解：联立方程组，解得，

    ∵x，y，z是非负数，

    ∴，

    解不等式组得0≤z≤，

    把 代入k=3x+y+5z，得 k=3(4-5z)+5z+1+5z=-5z+13，

    则当z=0时，k有最大值a＝13，当z= 时，k有最小值b=9，

    此时 ab=13×9=117．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

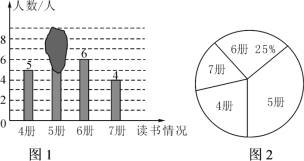
    【题目】老师随机抽查了本学期学生读课外书册数的情况，绘制成条形统计图(如图1)和不完整的扇形图(如图2)，其中条形统计图被墨迹遮盖了一部分．

    (1)求条形统计图中被遮盖的数，并写出册数的中位数；

    (2)随后又补查了另外几人，得知最少的读了6册，将其与之前的数据合并后，发现册数的中位数没有改变，则最多补查了____人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD，等边△ABE．已知∠BAC=30°，EF⊥AB，垂足为F，连接DF．

    （1）试说明AC=EF；

    （2）求证：四边形ADFE是平行四边形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在ABCD中，E、F分别是AB、DC边上的点，且AE=CF，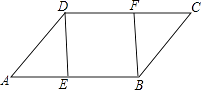

    （1）求证：△ADE≌△CBF．
    （2）若∠DEB=90°，求证：四边形DEBF是矩形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位，再向下平移4个长度单位得到点C.

    （1）用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;

    （2）若t=1时，平移线段AB，使点A、B到坐标轴上的点、处，指出平移的方向和距离，并求出点、的坐标；

    （3）若t=0时，平移线段AB至MN（点A与点M对应），使点Ｍ落在ｘ轴的负半轴上，三角形MNB的面积为4，试求点M、N的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一水池放水，先用一台抽水机工作一段时间后停止，然后再调来一台同型号抽水机，两台抽水机同时工作直到抽干．设从开始工作的时间为，剩下的水量为．下面能反映与之间的关系的大致图象是（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：

    （1）小明家到学校的路程是 米．

    （2）小明在书店停留了 分钟．

    （3）本次上学途中，小明一共行驶了 米．一共用了 分钟．

    （4）我们认为骑单车的速度超过 300 米/分就超过了安全限度．问：在整个上学途中哪个时间段小明的骑车速度最快，最快速度为多少，在安全限度内吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了提高产品的附加值，某公司计划将研发生产的1200件新产品进行精加工后再投放市场．现有甲、乙两个工厂都具备加工能力，公司派出相关人员分别到这两个工厂了解情况，获得如下信息：

    信息一：甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天；

    信息二：乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍．

    根据以上信息，求甲、乙两个工厂每天分别能加工多少件新产品．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD中，AB∥CD，BC⊥CD，E是AD的中点，连结BE并延长交CD的延长线于点F．

    （1）请连结AF、BD，试判断四边形ABDF是何种特殊四边形，并说明理由．

    （2）若AB=4，BC=5，CD=6，求△BCF的面积．

    查看答案和解析>>

    同步练习册答案