
【题目】如图,线段PQ=1,点P1是线段PQ的中点,点P2是线段P1Q的中点,点P3是线段P2Q的中点..以此类推,点pn是线段pn1Q的中点.
(1)线段P3Q的长为 ;
(2)线段pnQ的长为 ;
(3)求PP1+P1P2+P2P3+…+P9P10的值.
![]()
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据题意,可以写出线段P3Q的长,本题得以解决;
(2)根据题意,可以写出前几条线段的长,从而可以发现线段长度的变化规律,从而可以写出线段pnQ的长;
(3)根据图形和前面发现的规律,可以求而求得PP1+P1P2+P2P3+…+P9P10的值.
解:(1)由已知可得,
P1Q的长是![]() ,
,
P2Q的长是![]() ,
,
P3Q的长是![]() ,
,
(2)由已知可得,
P1Q的长是![]() ,
,
P2Q的长是![]() ,
,
P3Q的长是![]() ,
,
…,
则PnQ的长是![]() ,
,
(3)PP1+P1P2+P2P3+…+P9P10
=(1﹣P1Q)+(P1Q﹣P2Q)+(P2Q﹣P3Q)+…+(P9Q﹣P10Q)
=1﹣P1Q+P1Q﹣P2Q+P2Q﹣P3Q+…+P9Q﹣P10Q
=1﹣P10Q
=1﹣(![]() )10
)10
=1﹣![]()
=![]() .
.


科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图,请根据统计图中所提供的信息解答下列问题:
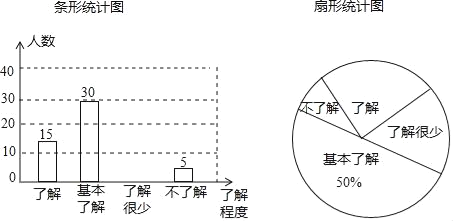
(1)接受问卷调查的学生共有 人,扇形统计图中“了解”部分所对应扇形的圆心角为 度;
(2)请补全条形统计;
(3)若该中学共有学生1200人,估计该中学学生对校园安全知识达到“了解”和“基本了解”程度的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
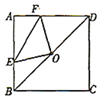
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据调查结果绘制成如下两幅不完整的统计图.
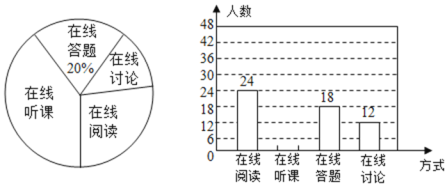
(1)求本次调查的学生总人数,并补全条形统计图;
(2)求扇形统计图中“在线讨论”对应的扇形圆心角的度数;
(3)该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西向的马路上有一个巡岗亭![]() ,巡岗员从岗亭
,巡岗员从岗亭![]() 出发以
出发以![]() 速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
速度匀速来回巡逻,如果规定向东巡逻为正,向西巡逻为负,巡逻情况记录如下:(单位:千米)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 |
|
|
|
|
|
|
|
(1)第几次结束时巡逻员甲距离岗亭![]() 最远?距离
最远?距离![]() 有多远?
有多远?
(2)甲巡逻过程中配置无线对讲机,并一直与留守在岗亭![]() 的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
的乙进行通话,问甲巡逻过程中,甲与乙保持通话的时长共多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
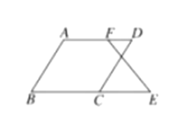
【题目】已知:如图![]() ,
,![]() ,那么
,那么![]() 成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
成立吗?为什么?下面是小丽同学进行的推理,请你将小丽同学的推理过程补充完整.
解:成立,理由如下:
![]() (已知)
(已知)
![]() ① (同旁内角互补,两条直线平行)
① (同旁内角互补,两条直线平行)
![]() (② )
(② )
又![]()
![]() (已知),
(已知),![]() (等量代换)
(等量代换)
![]() (③ )
(③ )
![]() (④ ).
(④ ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了更新体育器材,计划购买足球和篮球共100个,经市场调查:购买2个足球和5个篮球共需600元;购买3个足球和1个篮球共需380元。
(1)请分别求出足球和篮球的单价;
(2)学校去采购时恰逢商场做促销活动,所有商品打九折,并且学校要求购买足球的数量不少于篮球数量的3倍,设购买足球a个,购买费用W元。
①写出W关于a的函数关系式,
②设计一种实际购买费用最少的方案,并求出最少费用。
查看答案和解析>>
科目:初中数学 来源: 题型:
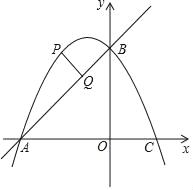
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com