
【题目】学校为了更新体育器材,计划购买足球和篮球共100个,经市场调查:购买2个足球和5个篮球共需600元;购买3个足球和1个篮球共需380元。
(1)请分别求出足球和篮球的单价;
(2)学校去采购时恰逢商场做促销活动,所有商品打九折,并且学校要求购买足球的数量不少于篮球数量的3倍,设购买足球a个,购买费用W元。
①写出W关于a的函数关系式,
②设计一种实际购买费用最少的方案,并求出最少费用。
【答案】(1)足球每个100元,篮球每个80元;(2)①W=18a+7200;②足球75个,篮球25个,费用最低,最低费用为8550元
【解析】
(1)根据“购买金额=足球数量×足球单价+篮球的数量×篮球单价”,在两种情况下分别列方程,组成方程组,解方程组即可;
(2) ①设购买足球a个 ,则购买篮球的数量为(100-a)个,则总费用(W)=足球数量×足球单价×0.9+篮球的数量×篮球单价×0.9,据此列函数式整理化简即可;
②根据购买足球的数量不少于篮球数量的3倍,且足球的数量不超过总数100,分别列一元一次不等式,组成不等式组,解不等式组求出a的范围;由于W和a的一次函数, k=18>0,W随a增大而增大,随a的减小而减小,所以当a取最小值a时,W值也为最小,从而求出W的最小值,即最低费用.
(1)解:设足球每个x元,篮球每个y元,由题意得
![]() 解得:
解得:![]()
答:足球每个100元,篮球每个80元
(2)解:①W=100×0.9a+80×0.9(100-a)=18a+7200,
答:W关于a的函数关系式为W=18a+7200,
②由题意得 ![]() ,解得:75≤a≤100
,解得:75≤a≤100
∵W=18a+7200,W随a的增大而增大,
∴a=75时,W最小=18×75+7200=8550元,
此时,足球75个,篮球25个,费用最低,最低费用为8550元.


科目:初中数学 来源: 题型:
【题目】某商店在今年2月底以每袋23元的成本价收购一批农产品准备向外销售,当此农产品售价为每袋36元时,3月份销售125袋,4、5月份该农产品十分畅销,销售量持续走高.在售价不变的基础上,5月份的销售量达到180袋.设4、5这两个月销售量的月平均增长率不变.
(1)求4、5这两个月销售量的月平均增长率;
(2)6月份起,该商店采用降价促销的方式回馈顾客,经调查发现,该农产品每降价1元/袋,销量就增加4袋,当农产品每袋降价多少元时,该商店6月份获利1920元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段PQ=1,点P1是线段PQ的中点,点P2是线段P1Q的中点,点P3是线段P2Q的中点..以此类推,点pn是线段pn1Q的中点.
(1)线段P3Q的长为 ;
(2)线段pnQ的长为 ;
(3)求PP1+P1P2+P2P3+…+P9P10的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察一组数据:2,4,7,11,16,22,29,…,它们有一定的规律,若记第一个数为a1,第二个数记为a2,…,第n个数记为an.
(1)请写出29后面的第一个数;
(2)通过计算a2-a1,a3-a2,a4-a3,…由此推算a100-a99的值;
(3)根据你发现的规律求a100的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在线段
在线段![]() 上,在
上,在![]() 的同侧作等腰
的同侧作等腰![]() 和等腰
和等腰![]() ,
,![]() 与
与![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .对于下列结论:
.对于下列结论:
①![]() ;②
;②![]() ;③
;③![]() .其中正确的是( )
.其中正确的是( )
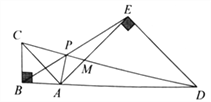
A. ①②③ B. ① C. ①② D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:6,BD平分∠ABC,点F在BC上,∠CDF=60°,∠ABD=25°.
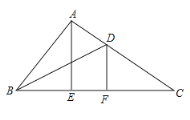
(1)求∠CAE的度数;
(2)求证:DF⊥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°, D是AB边上一点,且DB=DC,过BC上一点P(不包括B,C二点)作PE⊥AB,垂足为点E, PF⊥CD,垂足为点F,已知AD:DB=1:4,BC=![]() ,求PE+PF的长.
,求PE+PF的长.
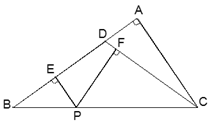
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com