
【题目】在△ABC中,AE⊥BC于点E,∠BAE:∠CAE=4:6,BD平分∠ABC,点F在BC上,∠CDF=60°,∠ABD=25°.
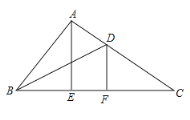
(1)求∠CAE的度数;
(2)求证:DF⊥BC.
【答案】(1)∠CAE=60°;(2)见解析
【解析】
(1)根据角平分线的定义可得∠ABC=2∠ABD=50°,然后根据垂直的定义可得∠AEB=∠AEC=90°,然后根据三角形的内角和定理即可求出∠BAE,然后根据已知比例式即可求出结论;
(2)根据三角形的内角和定理即可求出∠C,然后根据三角形外角的性质即可求出∠DFB=90°,最后根据垂直的定义即可证出结论.
解:(1)∵BD平分∠ABC,∠ABD=25°
∴∠ABC=2∠ABD=50°,
∵AE⊥BC
∴∠AEB=∠AEC=90°
∴∠BAE=180°-∠AEB-∠ABC=40°
∵∠BAE:∠CAE=4:6,
解得:∠CAE=60°
(2)在△CAE中,∠CAE=60°,∠AEC=90°
∴∠C=180°-∠CAE-∠AEC=30°
∵∠CDF=60°
∴∠DFB=∠CDF+∠C=90°
∴DF⊥BC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校为了更新体育器材,计划购买足球和篮球共100个,经市场调查:购买2个足球和5个篮球共需600元;购买3个足球和1个篮球共需380元。
(1)请分别求出足球和篮球的单价;
(2)学校去采购时恰逢商场做促销活动,所有商品打九折,并且学校要求购买足球的数量不少于篮球数量的3倍,设购买足球a个,购买费用W元。
①写出W关于a的函数关系式,
②设计一种实际购买费用最少的方案,并求出最少费用。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】感知:解不等式 ![]() .根据两数相除,同号得正,异号得负,得不等式组
.根据两数相除,同号得正,异号得负,得不等式组 ![]() 或不等式组
或不等式组![]() 解不等式组
解不等式组 ![]() ,得
,得 ![]() ;解不等式组
;解不等式组 ![]() ,得
,得 ![]() ,所以原不等式的解集为
,所以原不等式的解集为 ![]() 或
或![]() .
.
(1)探究:解不等式 ![]() .
.
(2)应用:不等式 ![]() 的解集是 .
的解集是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长的速度向
个单位长的速度向![]() 点匀速运动,同时点
点匀速运动,同时点![]() 从点
从点![]() 出发沿
出发沿![]() 方向以每秒
方向以每秒![]() 个单位长的速度向点
个单位长的速度向点![]() 匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点
匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点![]() 、
、![]() 运动的时间是
运动的时间是![]() 秒(
秒(![]() ).过点
).过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() .
.
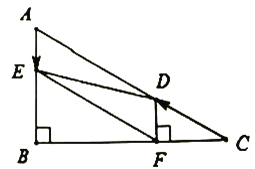
(1)![]() 的长是 ,
的长是 ,![]() 的长是 ;
的长是 ;
(2)在![]() 、
、![]() 的运动过程中,线段
的运动过程中,线段![]() 与
与![]() 的关系是否发生变化?若不变化,那么线段
的关系是否发生变化?若不变化,那么线段![]() 与
与![]() 是何关系,并给予证明;若变化,请说明理由.
是何关系,并给予证明;若变化,请说明理由.
(3)四边形![]() 能够成为菱形吗?如果能,求出相应的
能够成为菱形吗?如果能,求出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=80°,∠BAC=40°.
(1)尺规作图作出AB的垂直平分线DE,分别与AC、AB交于点D、E.并连结BD;(保留作图痕迹,不写作法)

(2)证明:△ABC∽△BDC.
查看答案和解析>>
科目:初中数学 来源: 题型:
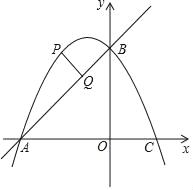
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件) | 100 | 110 | 120 | 130 | … |
月销量(件) | 200 | 180 | 160 | 140 | … |
已知该运动服的进价为每件60元,设售价为![]() 元.
元.
(1)请用含x的式子表示:①销售该运动服每件的利润是 元;②月销量是 件;(直接写出结果)
(2)设销售该运动服的月利润为![]() 元,那么售价为多少时,当月的利润最大,最大利润是多少?
元,那么售价为多少时,当月的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com