练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

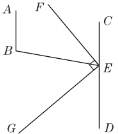
    【题目】推理计算：已知AB∥CD，∠B＝100°，EF平分∠BEC，EG⊥EF，求∠BEG和∠DEG的度数．

    【答案】∠BEG＝50°，∠DEG＝50°

    【解析】

    首先根据平行线的性质可得∠B＋∠CEB＝180°，进而可得∠CEB的度数，再根据角平分线的定义可得∠FEB的度数，然后再根据垂直定义可得∠GEB的度数；利用邻补角的性质可得∠BED，再根据角的和差关系可得∠DEG的度数．

    ∵AB∥CD，

    ∴∠B＋∠CEB＝180°，

    ∵∠B＝100°，

    ∴∠CEB＝180°100°＝80°，

    ∵EF平分∠BEC，

    ∴∠BEF＝80°÷2＝40°，

    ∵EG⊥EF，

    ∴∠FEG＝90°，

    ∴∠BEG＝90°40°＝50°，

    ∵∠CEB＝80°，

    ∴∠BED＝100°，

    ∴∠DEG＝100°50°＝50°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（本题满分10分）在一次蜡烛燃烧试验中，甲、乙两根蜡烛燃烧时剩余部分的高度 (厘米)与燃烧时间 (小时)之间的关系如图所示，其中乙蜡烛燃烧时与之间的函数关系式是.

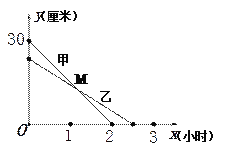
    (1)甲蜡烛燃烧前的高度是_________厘米,乙蜡烛燃烧的时间是________小时.

    (2)求甲蜡烛燃烧时与之间的函数关系式.

    (3)求出图中交点的坐标，并说明点的实际意义.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】线段AB和线段CD交于点O,OE平分∠AOC,点F为线段AB上一点(不与点A和点O重合)过点F作 FG//OE,交线段CD于点G,若∠AOD=110°,则∠AFG的度数为_____°.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东西向的马路上有一个巡岗亭，巡岗员从岗亭出发以速度匀速来回巡逻，如果规定向东巡逻为正，向西巡逻为负，巡逻情况记录如下：（单位：千米）

    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    第七次

    （1）第几次结束时巡逻员甲距离岗亭最远？距离有多远？

    （2）甲巡逻过程中配置无线对讲机，并一直与留守在岗亭的乙进行通话，问甲巡逻过程中，甲与乙保持通话的时长共多少小时？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，，那么成立吗？为什么？下面是小丽同学进行的推理，请你将小丽同学的推理过程补充完整．

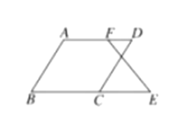
    解：成立，理由如下：

    （已知）

    ① （同旁内角互补，两条直线平行）

    （② ）

    又（已知），（等量代换）

    （③ ）

    （④ ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知有理数a、b在数轴上的对应点如图所示．

    （1）已知a=–2.3，b=0.4，计算|a+b|–|a|–|1–b|的值；

    （2）已知有理数a、b，计算|a+b|–|a|–|1–b|的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】学校为了更新体育器材，计划购买足球和篮球共100个，经市场调查：购买2个足球和5个篮球共需600元；购买3个足球和1个篮球共需380元。

    （1）请分别求出足球和篮球的单价；

    （2）学校去采购时恰逢商场做促销活动，所有商品打九折，并且学校要求购买足球的数量不少于篮球数量的3倍，设购买足球a个，购买费用W元。

    ①写出W关于a的函数关系式，

    ②设计一种实际购买费用最少的方案，并求出最少费用。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】感知：解不等式 ．根据两数相除，同号得正，异号得负，得不等式组 或不等式组 解不等式组 ，得 ；解不等式组 ，得 ，所以原不等式的解集为 或．

    （1）探究：解不等式 ．

    （2）应用：不等式 的解集是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在等腰△ABC中，AD⊥BC交直线BC于点D，若AD=BC，则△ABC的顶角的度数为_____．

    查看答案和解析>>

    同步练习册答案