
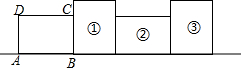
 如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )
如图,将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置,继续绕右下角的顶点按顺时针方向旋转90°至图②位置,以此类推,这样连续旋转2017次.若AB=4,AD=3,则顶点A在整个旋转过程中所经过的路径总长为( )| A. | 2017π | B. | 2034π | C. | 3024π | D. | 3026π |
分析 首先求得每一次转动的路线的长,发现每4次循环,找到规律然后计算即可.
解答 解:∵AB=4,BC=3,
∴AC=BD=5,
转动一次A的路线长是:$\frac{90π×4}{180}$=2π,
转动第二次的路线长是:$\frac{90π×5}{180}$=$\frac{5}{2}$π,
转动第三次的路线长是:$\frac{90π×3}{180}$=$\frac{3}{2}$π,
转动第四次的路线长是:0,
以此类推,每四次循环,
故顶点A转动四次经过的路线长为:$\frac{5}{2}$π+$\frac{3}{2}$π+2π=6π,
∵2017÷4=504…1,
∴顶点A在整个旋转过程中所经过的路径总长为:6π×504+2π=3026π,
故选D.
点评 本题主要考查了探索规律问题和弧长公式的运用,掌握旋转变换的性质、灵活运用弧长的计算公式、发现规律是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 售价x(元/千克) | 50 | 60 | 70 |
| 销售量y(千克) | 100 | 80 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 车型 | 甲 | 乙 | 丙 |
| 汽车运载量(吨/辆) | 5 | 8 | 10 |
| 汽车运费(元/辆) | 400 | 500 | 600 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com