
【题目】如图1,线段AB、CD相交于点O,连结AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于点M、N.试解答下列问题:
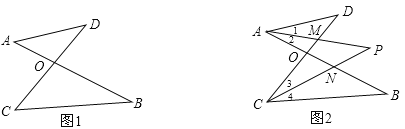
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系;
(2)仔细观察,在图2中“8字形”有多少个;
(3)图2中,当∠D=50°,∠B=40°时,求∠P的度数.
【答案】(1)∠A+∠D=∠C+∠B; (2)有6个;(3)∠P=45°;
【解析】
(1)根据三角形内角和定理即可得出∠A+∠D=∠C+∠B;
(2)根据“8字形”的定义,仔细观察图形即可得出“8字形”共有6个;
(3)先根据“8字形”中的角的规律,可得∠DAP+∠D=∠P+∠DCP①,∠PCB+∠B=∠PAB+∠P②,再根据角平分线的定义,得出∠DAP=∠PAB,∠DCP=∠PCB,将①+②,可得2∠P=∠D+∠B,进而求出∠P的度数;
(1)∵∠A+∠D+∠AOD=∠C+∠B+∠BOC=180°,∠AOD=∠BOC,
∴∠A+∠D=∠C+∠B;
(2)①线段AB、CD相交于点O,形成“8字形”;
②线段AN、CM相交于点O,形成“8字形”;
③线段AB、CP相交于点N,形成“8字形”;
④线段AB、CM相交于点O,形成“8字形”;
⑤线段AP、CD相交于点M,形成“8字形”;
⑥线段AN、CD相交于点O,形成“8字形”;
故“8字形”共有6个;
(3)∠DAP+∠D=∠P+∠DCP,①
∠PCB+∠B=∠PAB+∠P,②
∵∠DAB和∠BCD的平分线AP和CP相交于点P,
∴∠DAP=∠PAB,∠DCP=∠PCB,
①+②得:
∠DAP+∠D+∠PCB+∠B=∠P+∠DCP+∠PAB+∠P,
即2∠P=∠D+∠B,
又∵∠D=50°,∠B=40°,
∴2∠P=50°+40°,
∴∠P=45°;


科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
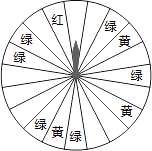
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说
,也就是说![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离,这个结论可以推广为
对应的点之间的距离,这个结论可以推广为![]() 表示数轴上
表示数轴上![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:对于任何有理数![]() 是否有最小值?如果有,写出最小值;如果没有,请说明理由.
是否有最小值?如果有,写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=72°,将△ABC绕点B按逆时针方向旋转得到△BDE(点D与点 A是对应点,点E与点C是对应点),且边DE恰好经过点C,则∠ABD的度数为

A. 36° B. 40° C. 45° D. 50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书是人类进步的阶梯!为爱护书一般都将书本用封皮包好,现有一本如图1的数学课本,其长为26cm、宽为18.5cm、厚为1cm,小海宝用一张长方形纸包好了这本数学书,他将封面和封底各折进去xcm封皮展开后如图(2)所示,求:
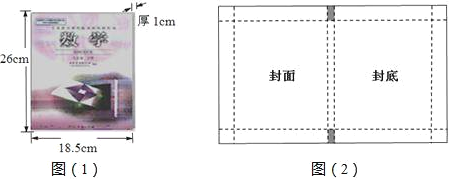
(1)则小海宝所用包书纸的面积是多少?(用含x的代数式表示)
(2)当封面和封底各折进去2cm时,请帮小海宝计算一下他需要的包装纸至少需要多少平方厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
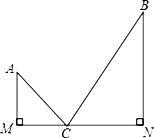
【题目】如图:知:AM⊥MN,BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点.若AM=3,BN=5,MN=15,则AC+BC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
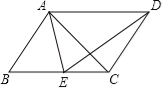
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com