
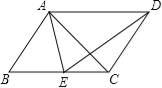
【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
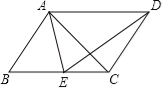
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
【答案】见解析
【解析】试题分析:从题中可知:(1)△ABC和△EAD中已经有一条边和一个角分别相等,根据平行的性质和等边对等角得出∠B=∠DAE即可证明.
(2)根据全等三角形的性质,利用平行四边形的性质求解即可.
(1)证明:∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC.
∴∠DAE=∠AEB.
∵AB=AE,
∴∠AEB=∠B.
∴∠B=∠DAE.
∵在△ABC和△AED中,
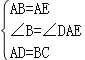 ,
,
∴△ABC≌△EAD.
(2)解:∵AE平分∠DAB(已知),
∴∠DAE=∠BAE;
又∵∠DAE=∠AEB,
∴∠BAE=∠AEB=∠B.
∴△ABE为等边三角形.
∴∠BAE=60°.
∵∠EAC=25°,
∴∠BAC=85°.
∵△ABC≌△EAD,
∴∠AED=∠BAC=85°.


科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x-1=0,② ![]() ③x-(3x+1)=-5 中,不等组
③x-(3x+1)=-5 中,不等组![]() 的关联方程是________
的关联方程是________
(2)若不等式组  的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
的一个关联方程的根是整数, 则这个关联方程可以是________(写出一个即可)
(3)若方程 3-x=2x,3+x= ![]() 都是关于 x 的不等式组
都是关于 x 的不等式组 ![]() 的关联方程,直接写出 m 的取值范围.
的关联方程,直接写出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AB=5,AC=6,BD=8. 
(1)求证:四边形ABCD是菱形;
(2)过点A作AH⊥BC于点H,求AH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课题组为了解全市八年级学生对数学知识的掌握情况,在一次数学检测中,从全市24000名八年级考生中随机抽取部分学生的数学成绩进行调查,并将调查结果绘制成如下图表:
分数段 | 频数 | 频率 |
| 20 | 0.10 |
60≤ | 28 | 0.14 |
70≤ | 54 | 0.27 |
80≤ |
| 0.20 |
90≤ | 24 | 0.12 |
100≤ | 18 |
|
110≤ | 16 | 0.08 |

请根据以上图表提供的信息,解答下列问题:
(1)表中![]() 和
和![]() 所表示的数分别为:
所表示的数分别为:![]() = ,
= ,![]() = ;
= ;
(2)请在图中,补全频数分布直方图;
(3)如果把成绩在90分以上(含90分)定为优秀,那么该市24000名八年级考生数学成绩为优秀的学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) 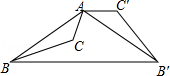
A.55°
B.65°
C.75°
D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)9+(﹣7)+10+(﹣3)+(﹣9)
(2)12+(﹣14)+6+(﹣7)
(3)﹣ ![]()
(4)﹣4.2+5.7+(﹣8.7)+4.2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连结BD并延长交EG于点T,交FG于点P,则GT=( ) 
A.![]()
B.2 ![]()
C.2
D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com