
 如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10.
如图,直角梯形ABCD的中位线EF=4,垂直于底的腰AB=5,则图中阴影部分的面积是10. 分析 过D作DM⊥EF于M,过C作CN⊥EF于N,根据梯形的中位线求出EF∥AD,求出四边形AEMD和四边形BENC都是矩形,根据矩形的性质得出DM=AE,CN=BE,求出DM+CN=AB=5,根据面积公式求出即可.
解答 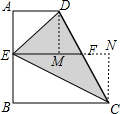
解:过D作DM⊥EF于M,过C作CN⊥EF于N,
∵梯形ABCD是直角梯形,EF为梯形的中位线,
∴EF∥AD,
∴∠A=∠AEM═∠DME=90°,∠B=∠CNE=∠BEF=90°,
∴四边形AEMD和四边形BENC都是矩形,
∴DM=AE,CN=BE,
∴DM+CN=AB=5,
∵直角梯形ABCD的中位线EF=4,
∴图中阴影部分的面积S=$\frac{1}{2}$×EF×(DM+CN)=$\frac{1}{2}$×4×5=10,
故答案为:10.
点评 本题考查了矩形的性质和判定,三角形的面积,梯形的性质的应用,能求出DM+CN=AB=5是解此题的关键,注意:梯形的中位线平行于两底,并且等于两底和的一半.


科目:初中数学 来源: 题型:填空题
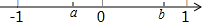 实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.
实数a、b在数轴上的对应点如图所示,化简$\sqrt{{a}^{2}}$•$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$的结果是-ab+b-a.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0 | B. | a | C. | $\sqrt{2}$ | D. | 不确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
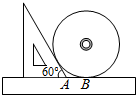 如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.
如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3cm,则此光盘的半径是3$\sqrt{3}$cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
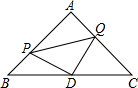 如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.
如图,△ABC是等腰直角三角形,∠A=90°,点P、Q分别是AB、AC上的一动点,且满足BP=AQ,D是BC的中点.求证:△PDQ是等腰直角三角形.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com