
 .
. 分析 根据题意可得y=3⊕x=$\left\{\begin{array}{l}{2(x≥3)}\\{-\frac{3}{x}(x<3,且x≠0)}\end{array}\right.$,再根据反比例函数的性质可得函数图象所在象限和形状,进而得到答案.
解答 解:由题意得y=3⊕x=$\left\{\begin{array}{l}{2(x≥3)}\\{-\frac{3}{x}(x<3,且x≠0)}\end{array}\right.$,
当x≥3时,y=2;当x<3且x≠0时,y=-$\frac{3}{x}$,图象如图: ,
,
故答案为:
点评 此题主要考查了反比例函数的图象性质和一次函数的图象性质,要掌握它们的性质才能灵活解题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 都有可能 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
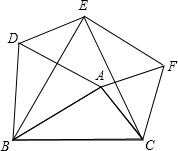 (1)感知:如图,分别以△ABC的三边为边长,在BC边的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE、EF,试猜想四边形ADEF的形状,并证明你的猜想.
(1)感知:如图,分别以△ABC的三边为边长,在BC边的同侧分别作三个等边三角形,即△ABD,△BCE,△ACF,连接DE、EF,试猜想四边形ADEF的形状,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
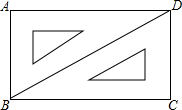 将两个相同的三角板如图所示拼成一个四边形ABCD(其中两条较长的直角边紧贴无间隙),若直角边AB=4cm,则点A与点C之间的距离为8cm(结果带根号)
将两个相同的三角板如图所示拼成一个四边形ABCD(其中两条较长的直角边紧贴无间隙),若直角边AB=4cm,则点A与点C之间的距离为8cm(结果带根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com