
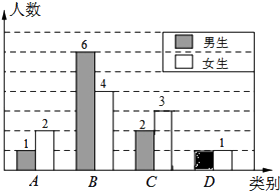
����Ŀ������ʦΪ���˽����̰༶ѧ�������ѧ��ǰԤϰ�ľ���������Ա��ಿ��ѧ��������Ϊ�ڰ���µĸ��ٵ��飬������������Ϊ���࣬A���ܺã�B���Ϻã�C��һ�㣻D���ϲ�������������Ƴ�����������������ͳ��ͼ���������ͳ��ͼ����������⣺ 
��1������ʦһ�������˶�����ͬѧ��
��2��C��Ů����3����D��������1������ͼ1����ͳ��ͼ����������
��3��Ϊ�˹�ͬ����������ʦ��ӱ������A���D��ѧ���и����ѡȡһλͬѧ���С�һ��һ������ѧϰ�������б���������ͼ�ķ��������ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�ĸ��ʣ�
���𰸡�
��1���⣺��6+4����50%=20����������ʦһ��������20��ѧ��
��2���⣺C��Ů����3����D��������1������������ͳ��ͼ
��3���⣺�����⻭����ͼ���£�
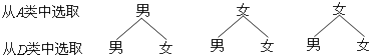
������ͼ���������п��ܳ��ֵĽ������6�֣���ÿ�ֽ�����ֵĿ�������ȣ���ѡ
��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ�Ľ������3�֣�
����P����ѡ��λͬѧǡ����һλ��ͬѧ��һλŮͬѧ��= ![]() =
= ![]()
����������1������B�����������Ů��10�ˣ���ռ�İٷֱ���50%�������������������2�����ݰٷֱȵ��������C����������������Ů����������ͬ�����D�������������������ɲ�ȫֱ��ͼ����3��������״ͼ����ʾ�����ֵ�����������������ø��ʹ�ʽ��⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ������ABCD�У�AB��DC����B=90�㣬AD=15��AB=16��BC=12����E�DZ�AB�ϵĶ��㣬��F������CD��һ�㣬����ED������AF���ڵ�G���ҡ�AGE=��DAB��
��1�����߶�CD�ij���
��2�������AEC����EGΪ���ĵ��������Σ����߶�AE�ij���
��3�������F�ڱ�CD�ϣ������C��D�غϣ�����AE=x��DF=y����y����x�ĺ�������ʽ����д��x��ȡֵ��Χ��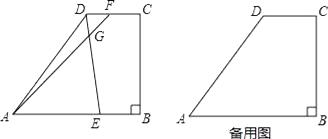
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+c��ͼ������ƽ��5����λ������ƽ��1����λ�ᾭ��ԭ�㣬��������ߵĶԳ�����x��Ľ���ĺ������ǣ� ��
A.2
B.��2
C.3
D.��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ȷ���ǣ� ��
A.a4��a2=a2
B.��a+b����a+b��=a2+b2
C.![]() ��
�� ![]() =
= ![]()
D.���� ![]() ����2=��4
����2=��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����POA1����P2A1A���ǵ���ֱ�������Σ�ֱ�Ƕ���P��P2�ں���y= ![]() ��x��0����ͼ���ϣ�б��OA1��A1A����x���ϣ����A�������ǣ� ��
��x��0����ͼ���ϣ�б��OA1��A1A����x���ϣ����A�������ǣ� �� 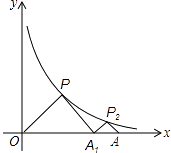
A.��4��0��
B.��4 ![]() ��0��
��0��
C.��2��0��
D.��2 ![]() ��0��
��0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+4��ͼ��A����3��0����B��5��4������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2���߶�AB�ڵ�һ�����ڵIJ�������һ����P������P��y���ƽ���ߣ����������ڵ�Q���Ƿ���ڵ�Pʹ�ı���BPCQ��������������ڣ��������P�����꼰��������ֵ����������ڣ�˵�����ɣ�
��3��x������������һ��D��1��0�����߶�AC���Ƿ���ڵ�M��ʹ��AOM�ס�ADC��������ڣ�ֱ��д����M�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���OΪ����ԭ�㣬������y=ax2��10ax+16a��a��0����x����A��B���㣬�����ߵĶ���ΪD���Գ�����x�ύ�ڵ�H����AB=2DH��
��1����a��ֵ��
��2����P�ǶԳ����Ҳ��������ϵĵ㣬����PD��PQ��x���ڵ�Q����N���߶�PQ�ϵĵ㣬����N��NF��DH�ڵ�F��NE��PD��ֱ��DH�ڵ�E�����߶�EF�ij���
��3���ڣ�2���������£�����DN��DQ��PB����DN=2QN��NQ��3����2��NDQ+��DNQ=90��ʱ����NC��PB���Գ��������������ڵ�C�����C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+ ![]() ��ֱ��AB���ڵ�A����1��0����B��4��
��ֱ��AB���ڵ�A����1��0����B��4�� ![]() ������D��������A��B����䲿���ϵ�һ�����㣨�����A��B�غϣ���ֱ��CD��y��ƽ�У���ֱ��AB�ڵ�C������AD��BD��
������D��������A��B����䲿���ϵ�һ�����㣨�����A��B�غϣ���ֱ��CD��y��ƽ�У���ֱ��AB�ڵ�C������AD��BD��
��1���������ߵı���ʽ��
��2�����D�ĺ�����Ϊm����ADB�����ΪS����S����m�ĺ�����ϵʽ���������Sȡ���ֵʱ�ĵ�C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB=��EDF=90�㣬��DEF=45�㣬AC=8cm��BC=6cm��EF=9cm����ͼ��2������DEF��ͼ��1����λ�ó�������1cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���B��������2cm/s���ٶ���BA�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ�ƶ�����PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s����0��t��4.5����
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE��
���ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com