
【题目】已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm.如图(2),△DEF从图(1)的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA匀速移动,当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动,DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).
解答下列问题:
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,
设四边形APEC的面积为y(cm2),求y与t之间的函数关系式,是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由;
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.
【答案】
(1)
解:∵点A在线段PQ的垂直平分线上,
∴AP=AQ;
∵∠DEF=45°,∠ACB=90°,∠DEF+∠ACB+∠EQC=180°,
∴∠EQC=45°;
∴∠DEF=∠EQC;
∴CE=CQ;
由题意知:CE=t,BP=2t,
∴CQ=t;
∴AQ=8﹣t;
在Rt△ABC中,由勾股定理得:AB=10cm;
则AP=10﹣2t;
∴10﹣2t=8﹣t;
解得:t=2;
答:当t=2s时,点A在线段PQ的垂直平分线上
(2)
解:如图1,过P作PM⊥BE,交BE于M,
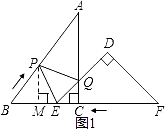
∴∠BMP=90°;
在Rt△ABC和Rt△BPM中,sinB= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴PM= ![]() ,
,
∵BC=6cm,CE=t,∴BE=6﹣t,
∴y=S△ABC﹣S△BPE= ![]() BCAC﹣
BCAC﹣ ![]() BEPM=
BEPM= ![]() 6×8﹣
6×8﹣ ![]() (6﹣t)×
(6﹣t)× ![]() t
t
= ![]() t2﹣
t2﹣ ![]() t+24=
t+24= ![]() (t﹣3)2+
(t﹣3)2+ ![]() ,
,
∵a= ![]() ,
,
∴抛物线开口向上;
∴当t=3时,y最小= ![]() ;
;
答:当t=3s时,四边形APEC的面积最小,最小面积为 ![]() cm2
cm2
(3)
解:假设存在某一时刻t,使点P、Q、F三点在同一条直线上;
如图2,
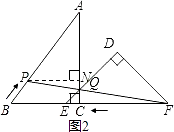
过P作PN⊥AC,交AC于N
∴∠ANP=∠ACB=∠PNQ=90°;
∵∠PAN=∠BAC,
∴△PAN∽△BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∴PN=6﹣ ![]() tAN=8﹣
tAN=8﹣ ![]() t,
t,
∵NQ=AQ﹣AN,
∴NQ=8﹣t﹣(8﹣ ![]() )=
)= ![]() ,
,
∵∠ACB=90°,B、C、E、F在同一条直线上,
∴∠QCF=90°,∠QCF=∠PNQ;
∵∠FQC=∠PQN,
∴△QCF∽△QNP;
∴ ![]() ,∴
,∴ ![]() =
= ![]() ;
;
∵0<t<4.5,∴ ![]() =
= ![]() ;
;
解得:t=1;
答:当t=1s,点P、Q、F三点在同一条直线上.
【解析】(1)因为点A在线段PQ垂直平分线上,所以得到线段相等,可得CE=CQ,用含t的式子表示出这两个线段即可得解;(2)作PM⊥BC,将四边形的面积表示为S△ABC﹣S△BPE即可求解;(3)假设存在符合条件的t值,由相似三角形的性质即可求得.


科目:初中数学 来源: 题型:
【题目】李老师为了了解所教班级学生完成数学课前预习的具体情况,对本班部分学生进行了为期半个月的跟踪调查,他将调查结果分为四类,A:很好;B:较好;C:一般;D:较差.并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 
(1)李老师一共调查了多少名同学?
(2)C类女生有3名,D类男生有1名,将图1条形统计图补充完整;
(3)为了共同进步,李老师想从被调查的A类和D类学生中各随机选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙A与x轴相交于C(﹣2,0),D(﹣8,0)两点,与y轴相切于点B(0,4).
(1)求经过B,C,D三点的抛物线的函数表达式;
(2)设抛物线的顶点为E,证明:直线CE与⊙A相切;
(3)在x轴下方的抛物线上,是否存在一点F,使△BDF面积最大,最大值是多少?并求出点F的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;② ![]() ;③DP2=PHPB;④
;③DP2=PHPB;④ ![]() .
.
其中正确的是 . (写出所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(0,6),B(8,0).点P从A点出发,以每秒1个单位的速度沿AO运动;同时,点Q从O出发,以每秒2个单位的速度沿OB运动,当Q点到达B点时,P、Q两点同时停止运动.
(1)求运动时间t的取值范围;
(2)整个运动过程中,以点P、O、Q为顶点的三角形与Rt△AOB有几次相似?请直接写出相应的t值.
(3)t为何值时,△POQ的面积最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】M为双曲线y= ![]() 上的一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+m于点D,C两点,若直线y=﹣x+m与y轴交于点A,与x轴相交于点B.
上的一点,过点M作x轴、y轴的垂线,分别交直线y=﹣x+m于点D,C两点,若直线y=﹣x+m与y轴交于点A,与x轴相交于点B.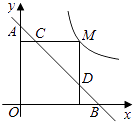
(1)求ADBC的值.
(2)若直线y=﹣x+m平移后与双曲线y= ![]() 交于P、Q两点,且PQ=3
交于P、Q两点,且PQ=3 ![]() ,求平移后m的值.
,求平移后m的值.
(3)若点M在第一象限的双曲线上运动,试说明△MPQ的面积是否存在最大值?如果存在,求出最大面积和M的坐标;如果不存在,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com