
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��A��0��6����B��8��0������P��A���������ÿ��1����λ���ٶ���AO�˶���ͬʱ����Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���
��1�����˶�ʱ��t��ȡֵ��Χ��
��2�������˶������У��Ե�P��O��QΪ�������������Rt��AOB�м������ƣ���ֱ��д����Ӧ��tֵ��
��3��tΪ��ֵʱ����POQ�����������ֵ�Ƕ��٣�
���𰸡�
��1��
�⣺�ߵ�B������Ϊ��8��0����
��OB=8��
�ߵ�Q��O��������ÿ��2����λ���ٶ���OB�˶�����Q�㵽��B��ʱ��P��Q����ͬʱֹͣ�˶���
��t��4��
���˶�ʱ��t��ȡֵ��ΧΪ��0��t��4
��2��
�⣺������ã�AP=t��OP=6��t��OQ=2t��
�ٵ�Rt��POQ��Rt��AOBʱ�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
�ڵ�Rt��POQ��Rt��BOAʱ�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ã�t= ![]() ��
��
��t= ![]() ��
�� ![]() ʱ���Ե�P��O��QΪ�������������Rt��AOB���ƣ�����������
ʱ���Ե�P��O��QΪ�������������Rt��AOB���ƣ�����������
��3��
�⣺��POQ�����= ![]() ��OP��OQ=
��OP��OQ= ![]() ��2t����6��t��=��t2+6t=����t��3��2+9��
��2t����6��t��=��t2+6t=����t��3��2+9��
�൱t=3ʱ����POQ�����������ֵ��9
����������1�������������OB�ij����õ��˶�ʱ��t��ȡֵ��Χ����2����Rt��POQ��Rt��AOB��Rt��POQ��Rt��BOA����������������������ε������г�����ʽ�����㼴�ɣ���3����t��ʾ����POQ����������ݶ��κ��������ʽ�ɣ�
�����㾫����������Ҫ�����˺�����ͼ������֪ʶ�㣬��Ҫ���պ�����ͼ������ֱ������ϵ�е�һϵ�е���ɣ�ͼ����ÿһ�����꣨x��y�������˺�����һ�Զ�Ӧֵ�����ĺ�����x��ʾ�Ա�����ij��ֵ��������y��ʾ������Ӧ�ĺ���ֵ������ȷ�����⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+4��ͼ��A����3��0����B��5��4������y�ύ�ڵ�C��
��1���������ߵĽ���ʽ��
��2���߶�AB�ڵ�һ�����ڵIJ�������һ����P������P��y���ƽ���ߣ����������ڵ�Q���Ƿ���ڵ�Pʹ�ı���BPCQ��������������ڣ��������P�����꼰��������ֵ����������ڣ�˵�����ɣ�
��3��x������������һ��D��1��0�����߶�AC���Ƿ���ڵ�M��ʹ��AOM�ס�ADC��������ڣ�ֱ��д����M�����ꣻ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������ABCD������ֱ�����ǰ��ֱ�Ƕ������������εĶ���D����ʹ���ǰ��Ƶ�D��ת��
��1�������ǰ���ת��ͼ1��λ��ʱ������CE��AF��������ϵ��������֤����
��2���ڣ�1���������£���DE��AE��CE=1�� ![]() ��3�����AED�Ķ�����
��3�����AED�Ķ�����
��3����BC=4����M�DZ�AB���е㣬����DM��DM��AC���ڵ�O�������ǰ��һ��DF���DM�غ�ʱ����ͼ2������OF= ![]() ����CN�ij���
����CN�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۵�����ABCD��ʹ��D����BC���ϵĵ�F�������ۺ�AE=5 ![]() ��tan��EFC=
��tan��EFC= ![]() ����BC= ��
����BC= �� 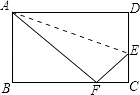
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB=��EDF=90�㣬��DEF=45�㣬AC=8cm��BC=6cm��EF=9cm����ͼ��2������DEF��ͼ��1����λ�ó�������1cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���B��������2cm/s���ٶ���BA�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ�ƶ�����PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s����0��t��4.5����
����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE��
���ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�����ͳһ�涨������������Ϊ5����1������Ϊ�ţ�2������Ϊ����3������Ϊ�����Ⱦ��4������Ϊ�ж���Ⱦ��5������Ϊ�ض���Ⱦ��ij���������ȡ��һ����ijЩ��Ŀ�����������������������Ƴ�����������������ͳ��ͼ�������ͼ����Ϣ��������и��⣺ 
��1�����ε��鹲��ȡ����Ŀ����������������ͳ�ƣ�
��2����ȫ����ͳ��ͼ��
��3������ͳ��ͼ��3��������������Ӧ��Բ�Ľ�Ϊ�㣻
��4�����������Ⱦ�ﵽ�ж���Ⱦ�������ϣ��������˽��л���������Ŀǰ��ͳ�ƣ�������Ƹ���ó���ֻ�ж��������˻�������һ��������365��ƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������и���
��1�����㣺�� ![]() ���У�0��6tan30��+��
����0��6tan30��+�� ![]() ����2+|1+
����2+|1+ ![]() |��
|��
��2���ⲻ��ʽ��  ����д���������������⣮
����д���������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���������߶��㶼��ֱ��y=x�ϣ������������߹���ԭ������ĶԳƣ����������������Ϊһ�ԡ��Ѻ������ߡ���

��1��������y=2��x-1��2+1��ͼ1��ʾ���뻭�����ġ��Ѻ������ߡ�����ֱ��д�����Ľ���ʽ��
��ȷ����������ú�ɫˮ����ڣ�
��2��һ�ԡ��Ѻ������ߡ�������һ�������ߵĽ���ʽΪy= -��x+h��2-h����ԡ��Ѻ������ߡ���y�ύ���ΪA��B����AB=n����A��B�غ�ʱ����n=0������������̽��n��h�Ĺ�ϵ��
�ٵ�h��0ʱ����ͼ2��ʾ����n��h�ĺ�����ϵʽ��
�ڵ�h��0ʱ����n��h�ĺ�����ϵʽ��
��3���ڣ�2���������£�Ҫʹ ![]() ��n��
��n�� ![]() ����ֱ��д��h��ȡֵ��Χ��
����ֱ��д��h��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������y= ![]() ��y=��
��y=�� ![]() ��ͼ��ֱ���l1��l2 �� ���P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ ��
��ͼ��ֱ���l1��l2 �� ���P��l1�ϣ�PC��x�ᣬ����ΪC����l2�ڵ�A��PD��y�ᣬ����ΪD����l2�ڵ�B�����PAB�����Ϊ �� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com