
 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,n),过点A作AB⊥x轴于点B,△AOB的面积为$\sqrt{3}$.
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A($\sqrt{3}$,n),过点A作AB⊥x轴于点B,△AOB的面积为$\sqrt{3}$.分析 (1)根据△AOB的面积为$\sqrt{3}$,可求出AB,得出点A的坐标,代入反比例函数解析式可求出k的值,继而得出反比例函数解析式;
(2)将点A的坐标代入一次函数解析式可求出m的值,求出点C的坐标,继而可根据勾股定理求出AC.
解答 解:(1)∵A的横坐标为$\sqrt{3}$,
∴OB=$\sqrt{3}$,
∵△AOB的面积为$\sqrt{3}$,
∴$\frac{1}{2}$×$\sqrt{3}$×AB=$\sqrt{3}$,
∴AB=2,
∴点A的坐标为:($\sqrt{3}$,2),
将($\sqrt{3}$,2)代入y=$\frac{k}{x}$,得k=2$\sqrt{3}$,
故反比例函数解析式为:y=$\frac{2\sqrt{3}}{x}$.
(2)把A($\sqrt{3}$,2)代入y=mx+1,得$\sqrt{3}$m+1=2,
解得:m=$\frac{\sqrt{3}}{3}$,
故一次函数解析式为:y=$\frac{\sqrt{3}}{3}$x+1.
令y=0,得0=$\frac{\sqrt{3}}{3}$x+1,
解得:x=-$\sqrt{3}$,即OC=$\sqrt{3}$,
则CB=OC+OB=2$\sqrt{3}$,
又∵AB=2,
∴AC=$\sqrt{{2}^{2}+(2\sqrt{3})^{2}}$=4.
点评 本题考查了反比例函数与一次函数的交点问题,解答本题的关键是求出点A的坐标,利用待定系数法求出两函数解析式,难度一般.


科目:初中数学 来源:2016-2017学年江苏省东台市第四教育联盟八年级下学期第一次月考数学试卷(解析版) 题型:单选题
四边形ABCD中,对角线AC、BD交于点O,给出下列四组条件:①AB∥CD,AD∥BC;②AB=CD,AD=BC;③AO=CO,BO=DO;④AB∥CD,AD=BC.一定能判定四边形ABCD是平行四边形的条件有 ( )
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
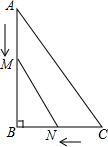 如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?
如图,在Rt△ABC中∠B=90°,AB=8m,BC=6m,点M、点N分别从A、C两点同时出发,分别沿AB、CB方向向点B匀速移动,它们的速度都是2m/s,问几秒后,△MBN的面积为Rt△ABC的面积的$\frac{1}{6}$?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为$\frac{12}{5}$.
如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,则点D到直线BC的距离为$\frac{12}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD.
如图,在Rt△ABC中,∠C=90°,AB的垂直平分线交BC于D,连结AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com