
ЁОЬтФПЁПдкаЁбЇЃЌЮвУЧвбОГѕВНСЫНтЕНЃЌГЄЗНаЮЕФЖдБпЦНааЧвЯрЕШЃЌУПИіНЧЖМЪЧ90Ёу.ШчЭМЃЌГЄЗНаЮABCDжаЃЌAD=9cmЃЌAB=4cmЃЌEЮЊБпADЩЯвЛЖЏЕуЃЌДгЕуDГіЗЂЃЌвд1cm/sЯђжеЕуAдЫЖЏЃЌЭЌЪБЖЏЕуPДгЕуBГіЗЂЃЌвдacm/sЯђжеЕуCдЫЖЏ,дЫЖЏЕФЪБМфЮЊts.
ЃЈ1ЃЉЕБt=3ЪБЃЌ
ЂйЧѓЯпЖЮCEЕФГЄЃЛ
ЂкЕБEPЦНЗжЁЯAECЪБЃЌЧѓaЕФжЕЃЛ
ЃЈ2ЃЉШєa=1,ЧвЁїCEPЪЧвдCEЮЊбќЕФЕШбќШ§НЧаЮ,ЧѓtЕФжЕЃЛ
ЃЈ3ЃЉСЌНгDP,жБНгаДГіЕуCгыЕуEЙигкDPЖдГЦЪБЕФaгыtЕФжЕ.

ЁОД№АИЁПЃЈ1ЃЉЂй5cmЃЛЂк![]() ЃЛЃЈ2ЃЉ3Лђ
ЃЛЃЈ2ЃЉ3Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЌt=4.
ЃЌt=4.
ЁОНтЮіЁПЪдЬтЗжЮі:(1) ЂйЕБt=3ЪБ,ИљОнТЗГЬ=ЫйЖШЁСЪБМф,ПЩЧѓГіDE=3,ШЛКѓгЩЙДЙЩЖЈРэПЩМЦЫуГіCE, ЂкЕБEPЦНЗжЁЯAECЪБ,ИљОнНЧЦНЗжЯпЕФаджЪПЩЕУ:ЕуPЕНECЕФОрРыЕШгкЕуPЕНADЕФОрРы,МДECБпЩЯЕФИпЕШгк4,РћгУЕШЛ§ЗЈПЩЧѓPC,дйРћгУЯпЖЮКЭВюЙиЯЕЧѓBP,ИљОнЫйЖШ=ТЗГЬЁТЪБМф,ПЩМЦЫуГіa,(2)ИљОнЯпКЭВюЙиЯЕ,ЙДЙЩЖЈРэАбPC,PE,CEгУКЌtЕФДњЪ§ЪНБэЪОГіРД,ШЛКѓИљОнЕШбќШ§НЧаЮЕФаджЪЗжЧщПіЬжТл,СаГіЙигкtЕФЗНГЬ,НтЗНГЬМДПЩЧѓНт,(3)ИљОнЕуCгыЕуEЙигкDPЖдГЦ,ПЩЕУDPДЙжБЦНЗжCE,ЫљвдDE=CD,PE=PC,ШЛКѓИљОнDE=CD,ПЩЯШМЦЫуГіt,ШЛКѓИљОнPE=PCПЩЧѓГіa.
ЪдЬтНтЮі:(1) ЂйЕБt=3ЪБ,дђDE=3,
дкRtЁїCDEжа, гЩЙДЙЩЖЈРэПЩЕУ:CE=![]() ,
,
ЂкЕБEPЦНЗжЁЯAECЪБ,ИљОнНЧЦНЗжЯпЕФаджЪПЩЕУ:ЕуPЕНECЕФОрРыЕШгкЕуPЕНADЕФОрРы,МДECБпЩЯЕФИпЕШгк4,Ыљвд![]() ,
,
Ыљвд![]() ,
,
ЫљвдPC=5,дђPB=BCЃPC=9Ѓ5=4,
гжвђЮЊPB=at=3t,
Ыљвд3t=4,НтЕУa=![]() ,
,
(2) дкRtЁїCDEжа, гЩЙДЙЩЖЈРэПЩЕУ:CE=![]() ,
,
ЫљвдPC=BCЃBP=9Ѓt,
гЩЙДЙЩЖЈРэПЩЕУ:PE=![]() ,
,
ЕБEC=PEЪБ,
![]() =
=![]() ,НтЕУt=3Лђt=9(ВЛЗћКЯЬтвт,ЩсШЅ),
,НтЕУt=3Лђt=9(ВЛЗћКЯЬтвт,ЩсШЅ),
ЕБEC=PCЪБ,
![]() =9Ѓt,НтЕУt=
=9Ѓt,НтЕУt=![]() ,
,
Ыљвдt=3Лђt=![]() ,
,
(3) вђЮЊЕуCгыЕуEЙигкDPЖдГЦ,
ЫљвдDPДЙжБЦНЗжCE,ЫљвдDE=CD=4,PE=PC,
ЫљвдDE=t=4,
вђЮЊBP=at,ЫљвдBP=4aЃЌ
ЫљвдPC=9Ѓ4a,
гЩЙДЙЩЖЈРэПЩЕУ:PE=![]() ,
,
![]() =9Ѓ4a,НтЕУa=
=9Ѓ4a,НтЕУa=![]() ,
,
Ыљвдa=![]() ,t=4.
,t=4.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁЯІС=32ЁуЃЌдђЁЯІСЕФгрНЧЮЊЃЈ ЃЉ
A.58Ёу
B.68Ёу
C.148Ёу
D.168Ёу
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК
ЃЈ1ЃЉЉ20+ЃЈЉ14ЃЉЉЃЈЉ18ЃЉЉ13
ЃЈ2ЃЉЉ4ЁТ ![]() ЉЃЈЉ
ЉЃЈЉ ![]() ЃЉЁСЃЈЉ30ЃЉ
ЃЉЁСЃЈЉ30ЃЉ
ЃЈ3ЃЉЉ22+|5Љ8|+24ЁТЃЈЉ3ЃЉЁС ![]()
ЃЈ4ЃЉЃЈ ![]() Љ
Љ ![]() Љ
Љ ![]() ЃЉЁС24ЁТЃЈЉ2ЃЉ3 ЃЎ
ЃЉЁС24ЁТЃЈЉ2ЃЉ3 ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
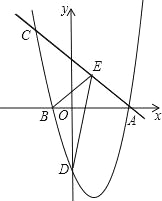
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=![]() +bxЉ4ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌЙ§ЕуAЕФжБЯпy=Љx+4НЛХзЮяЯпгкЕуCЃЎ
+bxЉ4ЃЈaЁй0ЃЉгыxжсНЛгкAЃЈ4ЃЌ0ЃЉЃЌBЃЈЉ1ЃЌ0ЃЉСНЕуЃЌЙ§ЕуAЕФжБЯпy=Љx+4НЛХзЮяЯпгкЕуCЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉдкжБЯпACЩЯгавЛЖЏЕуEЃЌЕБЕуEдкФГИіЮЛжУЪБЃЌЪЙЁїBDEЕФжмГЄзюаЁЃЌЧѓДЫЪБEЕузјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊx=2ЪЧЗНГЬx2-6x+m=0ЕФИљЃЌдђИУЗНГЬЕФСэвЛИљЮЊЃЈЁЁЁЁЃЉ
A.2
B.3
C.4
D.8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A. ЁА367ШЫжаБига2ШЫЕФЩњШеЪЧЭЌвЛЬьЁБЪЧБиШЛЪТМў
B. СЫНтвЛХњЕЦХнЕФЪЙгУЪйУќВЩгУШЋУцЕїВщ
C. вЛзщЪ§Он6ЃЌ5ЃЌ3ЃЌ5ЃЌ4ЕФжкЪ§ЪЧ5ЃЌжаЮЛЪ§ЪЧ3
D. вЛзщЪ§Он10ЃЌ11ЃЌ12ЃЌ9ЃЌ8ЕФЦНОљЪ§ЪЧ10ЃЌЗНВюЪЧ1.5
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com