
【题目】如图,∠1=75°,∠A=60°,∠B=45°,∠2=∠3,FH⊥AB于H.
(1)求证:DE∥BC;
(2)CD与AB有什么位置关系?证明你的猜想. 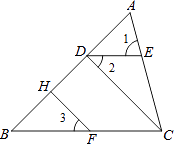
【答案】
(1)解:证明:∵∠A+∠B+∠ACB=180°,
∴∠ACB=180°﹣60°﹣45°=75°,
而∠1=75°,
∴∠1=∠ACB,
∴DE∥BC;
(2)解:CD⊥AB.理由如下:
∵DE∥BC,
∴∠2=∠BCD,
∵∠2=∠3,
∴∠3=∠BCD,
∴FH∥CD,
∵FH⊥AB,
∴CD⊥AB.
【解析】(1)先根据三角形内角和定理计算出∠ACB=75°,则∠1=∠ACB,然后根据同位角相等,两直线平行可判断DE∥BC;(2)由DE∥BC,根据平行线的性质得∠2=∠BCD,而∠2=∠3,所以∠3=∠BCD,则可根据内错角相等,两直线平行得FH∥CD,由于FH⊥AB,根据平行线的性质得CD⊥AB.
【考点精析】利用垂线的性质和平行线的判定与性质对题目进行判断即可得到答案,需要熟知垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.


科目:初中数学 来源: 题型:
【题目】如图所示,在一次夏令营活动中,小明从营地A点出发,沿北偏东60°方向走了500 ![]() m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点.
m到达B点,然后再沿北偏西30°方向走了500m到达目的地C点. 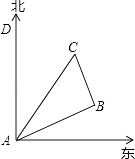
(1)求A、C两点之间的距离;
(2)确定目的地C在营地A的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(辽宁丹东)如图,直线OD与x轴所夹的锐角为30°,OA1的长为1,△A1A2B1、△A2A3B2、△A3A4B3…△AnAn+1Bn均为等边三角形,点A1、A2、A3…An+1在x轴的正半轴上依次排列,点B1、B2、B3…Bn在直线OD上依次排列,那么点Bn的坐标为 .
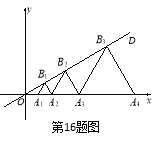
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级(1)班组织了一次朗读比赛,A队10人的比赛成绩(10分制)分别是:10、8、7、9、8、10、10、9、10、9.
(1)计算A队的平均成绩和方差;
(2)已知B队成绩的方差是1.4,问哪一队成绩较为整齐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小学,我们知道正方形具有性质“四条边都相等,四个内角都是直角”,请适当利用上述知识,解答下列问题:
已知:如图,在正方形ABCD中,AB=4,点G是射线AB上的一个动点,以DG为边向右作正方形DGEF,作EH⊥AB于点H.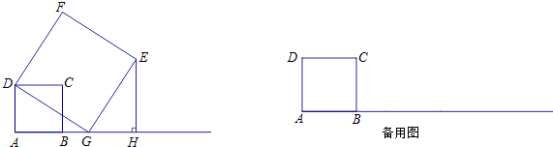
(1)填空:∠AGD+∠EGH=°;
(2)若点G在点B的右边.
①求证:△DAG≌△GHE;
②试探索:EH﹣BG的值是否为定值,若是,请求出定值;若不是,请说明理由.
(3)连接EB,在G点的整个运动(点G与点A重合除外)过程中,求∠EBH的度数;若点G是直线AB上的一个动点,其余条件不变,请直接写出点A与点F之间距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com