
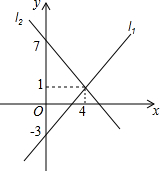 如图,两直线l1,l2的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{3}{2}x+7}\end{array}\right.$的解.
如图,两直线l1,l2的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{3}{2}x+7}\end{array}\right.$的解. 分析 先利用待定系数法分别求出两直线解析式,然后根据函数图象交点坐标为两函数解析式组成的方程组的解求解.
解答 解:设直线l1的解析式为y=kx+b,
把(0,-3)、(4,1)代入得$\left\{\begin{array}{l}{b=-3}\\{4k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=1}\\{k=-3}\end{array}\right.$,
所以直线l1的解析式为y=x-3,
同样方法可得直线l2的解析式为y=-$\frac{3}{2}$x+7
所以两直线l1,l2的交点坐标可以看作方程组$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{3}{2}x+7}\end{array}\right.$的解.
故答案为$\left\{\begin{array}{l}{y=x-3}\\{y=-\frac{3}{2}x+7}\end{array}\right.$.
点评 本题考查了一次函数与二元一次方程(组):函数图象交点坐标为两函数解析式组成的方程组的解.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:选择题
| A. | 了解居民对废电池的处理情况 | |
| B. | 为了制作校服,了解某班同学的身高情况 | |
| C. | 检测杭州的空气质量 | |
| D. | 了解某市居民的阅读情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2•a3=a6 | B. | 7a2-a2=7 | ||
| C. | -$(-\frac{1}{2})^{-2}$•(xy2)3=-4x3y6 | D. | (2m-n)2=4m2+n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 抛一枚硬币,正面朝上 | |
| B. | 打开电视,正在播放动画片 | |
| C. | 3个人分成两组,一定有2个人分在一组 | |
| D. | 随意掷两个均匀的骰子,上面的点数之和为6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
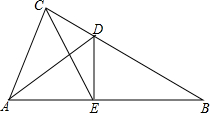 如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.
如图,在△ABC中,∠ACB=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB,垂足为点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com