
【题目】如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.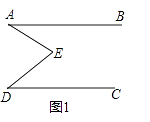
(1)探究猜想:
①若∠A=35°,∠D=30°,则∠AED等于多少度?
②若∠A=48°,∠D=32°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线EF与长方形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求写出证明过程)
【答案】
(1)解:①如图①,过点E作EF∥AB,

∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=35°,∠D=30°,
∴∠1=∠A=35°,∠2=∠D=30°,
∴∠AED=∠1+∠2=65°;
②过点E作EF∥AB,
∵AB∥CD,
∴AB∥CD∥EF,
∵∠A=48°,∠D=32°,
∴∠1=∠A=48°,∠2=∠D=32°,
∴∠AED=∠1+∠2=80°;
③猜想:∠AED=∠EAB+∠EDC.
理由:过点E作EF∥CD,
∵AB∥DC∴EF∥AB(平行于同一条直线的两直线平行),
∴∠1=∠EAB,∠2=∠EDC(两直线平行,内错角相等),
∴∠AED=∠1+∠2=∠EAB+∠EDC(等量代换).
(2)解:根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);

点P在区域②时,∠EPF=∠PEB+∠PFC;

点P在区域③时,∠EPF=∠PEB﹣∠PFC;

点P在区域④时,∠EPF=∠PFC﹣∠PEB.

【解析】(1)①过点E作EF∥AB,依据平行公理的推理可得到AB∥CD∥EF,然后依据平行线的性质以及∠AED=∠1+∠2求解即可;②过点E作EF∥AB,同理可得到问题的答案;③过点E作EF∥CD,同理可得到问题的答案;
(2)分为点P分别位于①、②、③、④四个区域,然后再根据平行线的性质进行求解即可得到结论.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
【题目】某校九年级进行立定跳远训练,以下是刘明和张晓同学六次的训练成绩(单位:m)
刘明:2.54,2.48,2.50,2.48,2.54,2.52
张晓:2.50,2.42,2.52,2.56,2.48,2.58
(1)填空:李明的平均成绩是 . 张晓的平均成绩是 .
(2)分别计算两人的六次成绩的方差,哪个人的成绩更稳定?
(3)若预知参加年级的比赛能跳过2.55米就可能得冠军,应选哪个同学参加?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,
的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,![]() )和(
)和(![]() ,
,![]() )在该图象上,则
)在该图象上,则![]() .其中正确的结论是 (填入正确结论的序号).
.其中正确的结论是 (填入正确结论的序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李到农贸批发市场了解到苹果和西瓜的价格信息如下:
水果品种 | 苹果 | 西瓜 |
批发价格 | 8元/公斤 | 1.6元/公斤 |
零售价格 | 10元/公斤 | 2元/公斤 |
他共用280元批发了苹果和西瓜共75公斤,
(1)请问小李批发的苹果和西瓜各多少公斤?
(2)若他当天把批发回来的苹果和西瓜按零售价格全部卖出,小李能赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线CD∥OA,点E、点F是OA上的动点,CE平分∠OCF,且满足∠FCA=∠FAC.
(1)若∠O=∠ADC,判断AD与OB的位置关系,证明你的结论.
(2)若∠O=∠ADC=60°,求∠ACE的度数.
(3)在(2)的条件下左右平行移动AD,∠OEC和∠CAD存在怎样的数量关系?请直接写出结果(不需写证明过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com